Drag Coefficient Calculator
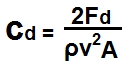
The drag coefficient calculator calculates the drag of an object as it moves through a fluid environment such as water or air.
The drag cofficient is a dimensionless unit (has no units) that is used to quantify the drag or resistance of an object in a fluid environment. Thus, the larger the drag cofficient of an item, the more drag or resistance that the fluid has on it. The smaller the coefficient, the less resistance that the fluid has on the object.
The drag coefficient is determined by 4 variables, the drag force, Fd, the fluid density of the fluid the object is passing through, ρ, the velocity that the object is travelling through this medium, v, and the reference area, A, of the object.
The drag force, Fd, is the amount of force which is produced in drag (opposition) to the object in motion. Drag force is the force opposite of the velocity vector. It is the force which opposes the movement of the object. The whole equation is referenced in terms of the direct relationship there is between drag coefficient and drag force.
The fluid density, ρ, is the mass density of the fluid which the object (car, plane) is travelling through. Water has greater fluid density than air, so an object travelling through water will have a greater drag coefficient than when travelling through air. The more dense a fluid is, the more difficult it is for an object to travel through, because of the greater density of the material. The less dense the fluid of an object, the easier it is for an object to travel through. You would think that as fluid density increases that drag increases. But this is not true. Being that the drag coefficient is directly proportional to fluid density, but since the drag coefficient is directly proportional to the drag force, which takes into account fluid density, it actually has an inverse relationship, since the drag coefficient is referenced in terms of the drag force. So as the fluid density increases, the drag coefficient decreases. Conversely, as the fluid density decreases, the drag coefficient increases. Again, since everything is referenced in terms of drag force, which takes into account, fluid density, if fluid density increases, drag coefficient must decreases, to counter the increase change. The unit of fluid density is kilograms per meters cubed (kg/m3).
The velocity, v, is the velocity of the object moving through the fluid. This is the speed of the object. The faster an object goes, the more drag it receives. This is because of Newton's 3rd law. For every action, there is an opposite and equal reaction. Since the car or plane is going faster forward, there will be an opposite, equal force push in the opposite direction for this action. Again, since the equation is referenced in terms of drag force, which takes into account velocity, there is an indirect relationship between the drag coefficient and velocity. As velocity increases, the drag coefficient decreases.The unit of velocity is meters per second (m/s).
The reference area, A, of an object is the area of the object which will be exposed to the air drag. Usually for automobiles and airplanes, this is the frontal area of the vehicle. The car's bumper and windshield will be the main area that drag affects. The larger the frontal surface area, the greater the drag. Since the equation again is referenced in terms of drag force which already takes into account surface area, the area has an indirect relationship with the drag coefficient. As frontal area increases, the drag coefficient decreases. The unit of surface area is meters squared (m2).
To use this calculator, a user fills in the 4 parameters, the drag force, Fd, the fluid density, ρ, the velocity, v, and the area, A, and clicks the 'Calculate' button. The resultant value will be automatically computed and shown. The resultant value, drag coefficient, again is unitless.
Car and airplane companies are always on campaigns to come up with new airplane and
car designs to create new vehicles with lower drag coefficients. Because the lower the drag coefficient, the less aerodynamic or hydrodynamic drag the
vehicle receives. When a vehicle receives less drag, its engines don't have to exert as much power to get past this fluid medium. Thus, it saves the vehicle
engine power, which translates into saved fuel. Thus, the lower the drag of the vehicle, the more fuel it is saved. So the vehicle receives more miles to the gallon.
Related Resources
