How to Calculate the Capacitance or the Inductance of a LC Resonant Circuit

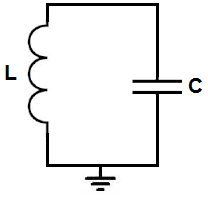
In this article, we show how to calculate the capacitance or inductance of an LC Resonant Circuit.

An LC resonant circuit is a circuit that will output a sine wave if fed in a square wave.

So the general formula to calculate the LC resonant frequency is shown below.

This formula would calculate the LC resonant frequency for you given the capacitance and inductance values.

But this may not be what you are looking for.

You may already know what resonant frequency you want and have one of the components, either the capacitor or the inductor.

You may just want to know what the third value should be to complete everything.

So basically to calculate either the capacitance or inductance, we need to isolate them in the above formula.

So that is what we do.

When we isolate the capacitance, C, in the formula, we get the following formula shown below.

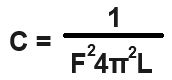
So, let's do an actual example, so you understand the practicality of this formula.

Let's say that we want to calculate the capacitance for an LC resonant frequency of 60Hz and we're using a 10mH inductor, what would the capacitance be in this case?

So plugging these values into the formula, we get, C= 1/(F²4π²L)= 1/(60²4π²(0.01)= 1/1419.7824= 0.000704333

.000704 is equal to .7mC or 700µF.

So in order to build an LC resonant circuit for 60Hz with a 10mH inductor, you would need approximately 700µF of capacitance. Being that 680µF are used, you can use this as an approximation or you can add 2 10µF capacitors in parallel with this 680µF capacitor to add up to 700µF, since capacitors add in parallel.

Let's now to go to the inductance value.

When we isolate the inductance, L, in the formula, we get the following formula shown below.

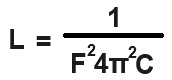
So let's go back to doing an example.

Let's say that we want to calculate the inductance for an LC resonant frequency of 60Hz and we're using a 700µF of capacitance, what would the inductance ve in this case?

So plugging these values into the formula, we get, L= 1/(F²4π²C)= 1/(60²4π²(0.0007)= 1/99.384768= 0.01

0.01 is equal to a 10mH inductor.

So this formula checks out with our previous example.

So using these formulas, we are able to calculate the capacitance or inductance needed for a particular resonant frequency.

Related Resources