How to Calculate the Voltage Across a Capacitor
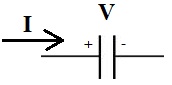
To calculate the voltage across a capacitor, the formula is:
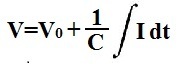
All you must know to solve for the voltage across a capacitor is C, the capacitance of the capacitor which is expressed in units, farads, and the integral of the current going through the capacitor.If there is an initial voltage across the capacitor, then this would be added to the resultant value obtained after the integral operation. Note that the initial value is denoted by, V0, if there is any.
So now that we've gone over the formula and each of the variables we must know, let's go over a few examples.
Example
A capacitor initially has a voltage across it of 4V. If the current going through a capacitor is 500sin(50t) and its capacitance is 2F, then what is
the voltage across the capacitor?
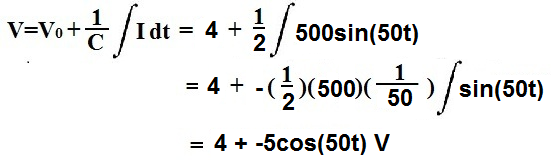
So the capacitor initally has 4V across it (this is 4VDC). We can pull out the
500 from the integral. Doing the integral math, from the frequency of the current signal, we
get (1/50).Being that the integral of a sine function is negative cosine, this is why there is a
negative sign in the math operation. Computing the results gives us the final answer of,
4 + -5cos(50t) V.
Another Example
If the current going through a capacitor is 10cos(1000t) and its capacitance is 5F, then what is
the voltage across the capacitor?
(*Initial Conditions: The capactior has 0 volts across it initially)
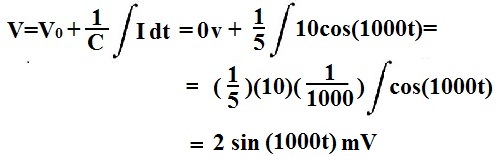
In this example, there is no initial voltage, so the initial voltage is 0V. We
can pull the 10 from out of the integral. Doing the integral math, we pull out (1/1000). The
integral of a cosine function is a sine function. Doing
the math, this gives us 0.002sin(1000t)V or 2sin(1000t) mV.
To calculate this result through a calculator to check your answers or just calculate problems, see our online calculator,
Capacitor Voltage Calculator. This calculator lets you put in
the current and capacitance to calculate the voltage across a capacitor.
