Multiplying Significant Figures (Sig Fig) Calculator

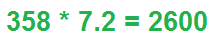
This Multiplying Significant Figures Calculator computes the product of the numbers entered in and places the resultant value into proper significant figures.
Significant figures, or digits, are the values in a number that can be counted on to be accurate. Significant digits in a number are those values which can be known with certainty or a high degree of confidence, while insignificant digits are those which we do not trust as very accurate.
Significant digits are used extensively during measurements. Different measurement tools can record measurements of differing accuracy. Some measurement tools can record much more in detail than other measuring tools. For example, if we have a ruler that only measures centimeters, we can measure to one-hundredth of a meter. If we now change the ruler and get one which measures millimeters, we can measure to one-thousandth of a meter. Thus, we can have an extra significant digit, because the ruler is more detailed and allows for more accuracy of measurement.
It is important to be honest when making a measurement, so that the resulant value does not appear to be more accurate than the equipment used to make the measurement allows. And how we make the recorded value honest is by controlling the number of digits, or significant figures, used to report the measurement. The recorded value cannot have more significant digits than the measuring tool allows. This is why using the proper amount of significant digits is so important.
When multiplying significant digits, the amount of significant figures in the final product is determined by the number of significant digits in each of the multiplicands. The product can only have as many significant digits as the multiplicand with the least amount of significant digits. So if one of the multiplicands has 2 significant digits and the other has 3 significant digits, for example, the product of the multiplication operation can only have 2 significant digits in it. So, the product can only have as many significant digits as the multiplicand with the least amount of significant digits.
This is the only rule to follow when multiplying numbers and keeping proper significant figures. It must be determined how many significant figures each of the multiplicands has. Once this is determined, the product can only have as many significant figures as the multiplicand with the least amount of significant digits.
To use this calculator, a user simply enters in the multiplication problem into the text box using the "*" as the multiplication operand, and clicks the 'Calculate' buton. The resultant value in proper significant figures will be automatically computed and displayed.
Being that electronics, like any other science, deals with measurements, knowing how to multiply significant figures may be important. Depending
on the measuring tool in use determines how accurate it can measure. Using the proper number of
significant figures may be extremely important.
Examples
What is 345 * 7.8?
345 * 7.8= 2700
Being that 345 has 3 significant digits and 7.8 has 2 significant digits, the product can only have 2 significant digits.
What is 75 * 0.0003?
75 * 0.003 = 0.2
Being that 75 has 2 significant digits and 0.0003 has 1 significant digit, the product can only have 1 significant digit.
What is 2.0 * 3.00?
2.0 * 3.00= 6.0
Being that 2.0 has 2 significant digits and 3.00 has 3 significant digits, the product can only have 2 significant digits.
Related Resources
Dividing Significant Figures Calculator
Adding Significant Figures Calculator
Subtracting Significant Figures Calculator
Significant Figures (Sig Fig) Calculator
Significant Figures Rounding Calculator
