Mutual Inductance Calculator
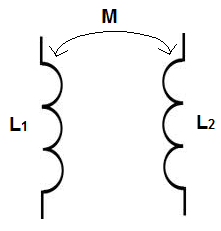
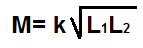
Coupling coefficient, k, must be between values 0 and 1.
The mutual inductance calculator calculates the mutual inductance of 2 inductors with a coupling coefficient of k, according to the formula shown above.
A user enters the coupling coefficient, K, inductor L1, and inductor L2, and the result will automatically be calculated and shown. The inductance result which is displayed above is in unit henry (H).
Mutual inductance is affected by the inductance values of the 2 inductors and the coupling coefficient between these 2 inductors. The larger the value of the inductances of the inductors, the larger the mutual inductances. And conversely, the smaller the inductances, the smaller the mutual inductance total. So, for instances, 2 inductors that have inductance values of 2H and 4H will have a much larger mutual inductance than 2 inductors that have inductance values of 2µH and 4µH, if all factors are the same. The other factor that affects mutual inductance is the coupling coefficient. Coupling coefficient is a value that ranges from 0 to 1. The coupling coefficient is the fraction of total flux from one coil linking to the other coil. For example, if all the flux of inductor L1 links to inductor L2, then the coupling coefficient, k, is equal to 1. If half the flux of one coil links to the other, then k equals 0.5. If none of the flux links to the other coil, k equals 0, and the mutual inductance is 0. So k= flux linkages between L1 and L2/flux produced by L1. K has no units. The greater the value of k, the greater the mutual inductance. The lower the value of k, the lower the mutual inductance. K has no units, because it is a ratio of 2 identical units, which is magnetic flux. The coefficient coupling is increased by placing the coils close together. A high value of K, called tight coupling, allows the current in one coil to induce more voltage in the other coil. Loose coupling, with a low value of k, has the opposite effect and induces less voltage.
Mutual inductance calculation is very important in circuits that have inductors in them or even wires close together that can act as inductors.
Example Calculation
Calculate the mutual inductance of a circuit which has L1=20H and L2=5H with a coupling coefficient, k, of 0.75.
Related Resources
Parallel and Series Inductor Calculator
Inductance Calculator
Inductor Energy Calculator
Inductor Impedance Calculator
Ferrite Core Inductor Calculator
