Polar to Rectangular Form Conversion Calculator
Formula
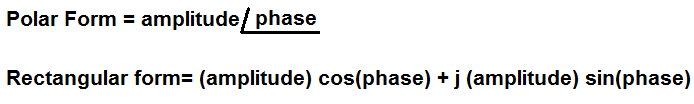
Example
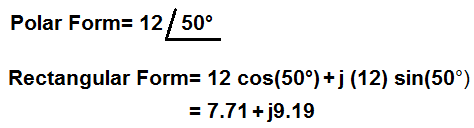
This polar to rectangular form conversion calculator converts a number in polar form to its equivalent value in rectangular form.
Polar, or phasor, forms of numbers take on the format, amplitude < phase. The phase is specified in degrees.
Rectangular forms of numbers take on the format, x + jy, where x and y are numbers. The x portion of the number represents the real part of the expression and the y part represents the imaginary part of the expression.
Polar forms of numbers can be converted into their rectangular equivalents by the formula, Rectangular form= amplitude * cos(phase) + j(amplitude) * sin(phase). This is all based off the fact that the polar form takes on the format, amplitude < phase.
So, for example, let's take the expression in polar form, 12 < 55°. We want to convert this into its equivalent rectangular form. So, to do this, we take the formula and plug in the values, giving us, rectangular form= 12 cos(55°) + j(12)sin(55°)= 6.88 + j9.83.
And that's all that's required in order to convert from polar form to rectangular form.
Usually, in electronics, polar forms are used in express components in AC circuit analysis. For example, if you are doing AC circuit analysis, one of the things that is required to do this is to convert the circuit from the time domain to the frequency domain, so that the circuit can be analyzed in the frequency domain. Therefore, the power source of the circuit is converted from the expression in the time domain to its expression in the frequency domain. In the frequency domain, the power source is expressed in polar form. So in situations like these, you will encounter numbers in polar form. This calculator can be useful in expressing this polar form to another form, like rectangular form.
This calculator is able to take into account phases less than 0° as well as phases greater than 360°, so any value phase can be entered, such as -45° or 725°. Even though one complete cycle of a sine or cosine wave lasts 360°, it can occur at any phase angle. However, this calculator finds the equivalent of the phase entered in between the 0° to 360° phase by either adding 360° one or several times to a negative number to bring it into this range or subtracting 360° one or several times to a positive number to bring it into this range. The calculator uses the principle that the phase of an angle plus or minus 360 degrees is equivalent. This is because since a sine or cosine function constantly repeats itself every cycle and one cycle is 360°, if you add or subtract 360° either one time or many times, you will get the same value.
Since the only 2 components of a number expressed in polar form are the amplitude and the phase of the signal, these are the only
2 inputs required for the calculator to compute the equivalent number in rectangular form.
Related Resources
Rectangular to Polar Form Conversion Calculator
Rectangular to Exponential Form Conversion Calculator
Polar to Exponential Form Conversion Calculator
Exponential to Rectangular Form Conversion Calculator
Exponential to Polar Form Conversion Calculator
