Why Transistors Need Biasing

Transistors need biasing in order to function correctly.
You may think, why is biasing even necessary?
Why don't we just feed into the transistors the AC signal that we want to amplify, in the case of an application for amplification and not worry about biasing and DC power.
There's a few reasons why we do need DC biasing.
First of all, if you simply fed an AC signal to a transistor, such as a BJT transistor, without DC power, you wouldn't get the desired effect you are looking for, such as an amplified sine wave as the output.
Transistors are essentially composed of junctions that function as diodes.
If you fed an AC voltage signal to a transistor, the transistor would only turn on during the positive portion of the sine wave that is greater than 0.7V. Everything below +0.7V would be cut off because during this portion of the sine wave, the transistor wouldn't have sufficient power. BJT transistors need at least +0.7V applied to the base in order for the transistor to turn on. Thus, for an AC signal such as a sine wave, the transistor would be only on for a small portion of the sine wave and be off for most of the sine wave cycle, including the positive portion below 0.7V.
However, if we bias the transistor in which we feed it sufficient base voltage, we have the transistor always in an ON state. If we supply enough voltage to the transistor, the whole sine wave signal will be output without any clipping to the signal.
Another reason we need DC biasing is because of the inherent nature of transistors.
Unfortunately, the manufacturing process of transistors do not produce identical transistors, and transistors are not inherently stable. No two transistors will have the same identical parameters, one of the most important being β, which represents the gain of the transistor. Also not only are the transistors not identical in terms of parameters such as β, but for each individual transistor, β is not stable, changed due to changes in temperature.
Thus, due to the fact that transistors can have widely differing β values and that the β values themselves can change due to changes in temperature, we must create a biasing circuit in which the transistor gives stable, predictable output despite these changes to β.
If we give the transistor the correct DC voltages and connect the right resistances to the transistors, we can have the transistor provide stable, predictable gain despite widely differing β values.
This is another reason why biasing of transistors is necessary.
It allows us to have a transistor with a stable, measured output that can be the same output despite the transistor used.
Thus, if we are mass producing a electronic product that has such a transistor, each transistor produces the same output, despite possibly widely varying parameter values. Thus, each product predictably functions the same. Imagine each iphone that apple manufactures functions completely different because of the inherent unstable nature of transistors. That would be bad.
So biasing is something that you just need to learn.
Some biasing methods are very effective and produce very stable outputs.
Other biasing methods are very poor and make transistors circuits that can produce very different outputs if the β value of the transistor is very different.
Thus, how you bias a transistor circuit makes a great difference.
How you can determine how stable a transistor biasing method is is simply based on math.
DC biasing can easily be calculated with formulas.
The ultimate goal of a transistor is stable, predictable current and/or voltage gain.
If we get very close voltage and current outputs despite widely varying β values, we know that our biasing protects against changes in β and, thus, gives good predictable output.
Two of the best methods of biasing a transistor circuit is the two-supply emitter bias method and the voltage divider bias method.
The two-supply emitter bias method is a little bit more complicated, as it requires 2 separate DC voltage supplies. Thus, we will focus on the voltage divider bias method.
This is a method that uses one power supply and largely relies on using appropriate resistor values to allow for stable, predictable transistor outputs despite possibly widely varying transistor β values.
So let's see how this applies in real life with a real transistor circuit with DC biasing with the voltage divider method.
Only basic math is needed.
So the circuit we will work with is shown below.
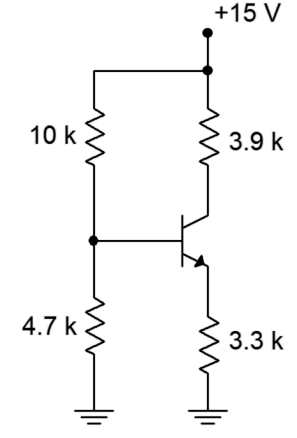
So now we have to do the math.
We're going to do the math first for a β of 100. And then we will calculate for a much higher value of 200 and see what difference we get.
Being that BJTs are current amplifying devices, we can judge the gain by measuring the difference in collector currents (IC). 4
So let's do the math now.
To obtain the voltage, VTH, we use the formula, VTH= VCCR2/(R1 + R2) = 15V(4.7KΩ)/(10KΩ + 4.7KΩ)= 4.8V
RTH= R1 || R2= R1R2/(R1 + 4.7KΩ)= 3.2KΩ
IC = VTH - VBE/RE + RTH/β = (4.8V - 0.7V)/(3.3KΩ + 3.2KΩ/100) = 1.230492 mA
Now let's substitute the last equation for a β of 200, which is double the 100 we had before.
IC = VTH - VBE/RE + RTH/β = (4.8V - 0.7V)/(3.3KΩ + 3.2KΩ/200) = 1.236429 mA
So let's do the math between the difference of IC at a β of 100 (IC of 1.230492 mA) and IC at a β of 200 (IC of 1.236429 mA).
You can see that it is not a great difference between the two currents even though there is a large difference in β.
Doing the math, the difference yields the following.
1.236429 mA - 1.230492 mA/1.230492 mA = 0.005937/1.230492 = 0.00482 = 0.4%.
That represents less than a half of a percent difference, even though the difference in β is 100%.
This shows that that the voltage divider bias method is an effective method to give the BJT power and also to protect against changes in β.
What really achieves this is the high value of the emitter resistor (RE).
When RE is a high value in comparison to RTH/β, it leads to great stability and stable gain despite large differences in β that different transistors may have.
Related Resources
