Calculadora de Ensayo de Bernoulli

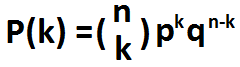
Esta calculadora de ensayo de Bernoulli calcula la probabilidad de que ocurra un evento.

La fórmula para calcular el resultado del ensayo de bernoulli se muestra a continuación:

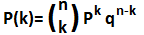
El ensayo de Bernoulli se calcula multiplicando el coeficiente binomial con la probabilidad de éxito de la potencia k multiplicada por la probabilidad de falla de la potencia n-k.

representa el coeficiente binomial. El coeficiente binomial representa el número total de combinaciones diferentes que podemos tomar k elementos de un total de n selecciones. Por ejemplo, si tenemos un total de 7 elementos y queremos elegir 5 elementos de esos 7, entonces n = 7 y k-5, y el coeficiente binomial sería igual a 21. Esto significa que hay 21 combinaciones posibles diferentes que podemos organizar 5 elementos cuando se toma de un total de 7 elementos.

p^k representa la probabilidad de que ocurra el evento. Representa la tasa de éxito con la que se produce el evento.

q^n-k representa la probabilidad de que el evento no ocurra. Representa la tasa de fallas del evento.

Cuando tomamos todas estas variables y las multiplicamos, obtenemos el resultado del ensayo de bernoulli. El ensayo de Bernoulli representa la probabilidad de éxito (que ocurra un evento).

El cálculo de ensayo de Bernoulli solo se puede realizar en las siguientes circunstancias.

1. 2 resultados solamente- Cuando solo hay 2 resultados posibles, la mayoría de las veces se expresa como éxito o fracaso. Esto puede representar muchas resultados como cara o cruz, gane o pierda, vaya o no vaya. Solo se puede hacer cuando hay exactamente 2 resultados. La mayoría de las veces se expresará como éxito o fracaso.
2. Cada prueba debe ser independiente : Cada prueba (cada vez que ocurre el evento) debe ser independiente entre sí. Esto significa que los eventos son completamente independientes; no dependen del ensayo anterior ni del ensayo posterior. Un ejemplo clásico es cara o cruz. Cada giro es independiente de todos los demás.
3. La probabilidad de éxito es la misma para cada prueba : La probabilidad de que ocurra el evento o de que el resultado deseado tenga éxito debe ser la misma. Por ejemplo, por cada lanzamiento de una moneda, siempre hay una tasa de éxito del 50% para obtener cara. En otras palabras, la probabilidad de que ocurra un evento debe ser la misma, no diferente, para cada ensayo.

Si se cumplen todas estas condiciones, podemos aplicar el ensayo de Bernoulli para encontrar el resultado porcentual de que ocurrirá un evento.

Para ilustrar el ensayo de bernoulli, veamos un ejemplo real en el que se utilizaría el ensayo de bernoulli.

528/5000 Digamos que hay un examen en el que aprueban el 60% de los alumnos. Este es el examen de ingreso para estudiantes de primer año. Si 7 estudiantes de primer año toman el examen, ¿cuál será la probabilidad de que 5 aprueben? En este ejemplo, n= 7, k= 5 y la tasa de éxito es 60% o 0,6. La tasa de fallas entonces será 1-.6 = .4 o 40%. Usando estos números, los conectamos a la fórmula. El coeficiente binomial de n= 7 y k= 5 será 21. Entonces tenemos P (k) = 21(.6)⁵(.4)²= .2613 o 26,13%. Este 26,13% es la tasa de éxito que 5 de cada 7 estudiantes de primer año aprobarán el examen.

Para usar esta calculadora, un usuario simplemente ingresa los valores n y k, solo con la probabilidad de que ocurra el evento. A continuación, hace clic en el botón "Calcular" y el cálculo del ensayo de bernoulli resultante se calculará y mostrará automáticamente.

El ensayo de Bernoulli se puede utilizar para cualquier cálculo científico.

Recursos Relacionados