Capacitor Discharging- Explained

The Capacitor discharging cycle that a capacitor goes through is the cycle, or period of time, it takes for a capacitor to discharge of its charge and voltage.
In this article, we will go over this capacitor discharging cycle, including:
Capacitor Discharge Equation
Capacitor Discharging Graph
Capacitor Discharge Equation
The Capacitor Discharge Equation is an equation which calculates the voltage which a capacitor discharges to after a certain time period has elapsed.
Below is the Capacitor Discharge Equation:

Below is a typical circuit for discharging a capacitor.
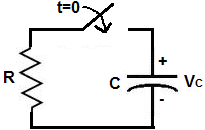
To discharge a capacitor, the power source, which was charging the capacitor,
is removed from the
circuit, so that only a capacitor and resistor can connected together in series. The capacitor drains
its voltage and current through the resistor.
Variables in Capacitor Discharge Equation
Taken into account the above equation for capacitor discharge and its accompanying circuit, the variables which make up the equation are explained below:
- VC- VC is the voltage that is across the capacitor after a certain time period has elapsed.
- V0- V0 is the initial voltage across the capacitor before the discharging begins where it's connected in series with a resistor in a closed circuit. In simple terms, this is the voltage that the capacitor initially has before the discharge process begins.
- Time, t- Time, t, is the period of time which has elapsed since the discharge process has begun. t is measured in unit seconds. It is a very important parameter in this equation because it determines how much the capacitor discharges. The more time that has elapsed, the more the capacitor will discharge. Conversely, the less time that has elapsed, the less the capacitor will have discharged.
- Resistance, R- R is the resistance of the resistor to which the capacitor is connected to in the circuit, as shown in the diagram above. This affects the discharging process in that the greater the resistance value, the slower the discharge, while the smaller the resistance value, the quicker the discharge, and, thus, the lower the amount of voltage, VC, across the capacitor.
- Capacitance, C- C is the capacitance of the capacitor in use. C affects the discharging process in that the greater the capacitance, the more charge a capacitor can hold, thus, the longer it takes to discharge, which leads to a greater voltage, VC. Conversely, a smaller capacitance value leads to a quicker discharge, since the capacitor can't hold as much charge, and thus, the lower VC at the end.
These are all the variables explained, which appear in the capacitor discharge equation.
Again, if you want a quicker discharge time for a RC circuit, use a small resistance value for the resistor, a small capacitance value for a capacitor, and a lower initial voltage across the capacitor before discharge begins, for the variables you can control, for the reasons explained above.
If you want a longer discharge time for a RC circuit, use a large resistance value, a large capacitance value, and a large initial voltage across the capacitor.
The discharge time which you'll need depends on the specific application for which
the RC circuit is used for.
Capacitor Discharging Graph
The Capacitor Discharging Graph is the a graph that shows how many time constants it takes for a capacitor to discharge
to a given percentage of the applied voltage.
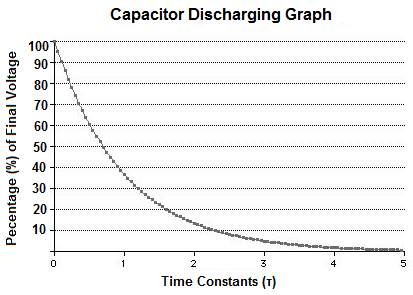
A capacitor discharging graph really shows to what voltage a capacitor will discharge to after a given amount of time has elapsed.
Capacitors take a certain amount of time to discharge. Discharging a capacitor is not instantaneous. Therefore, calculations are taken in order to know when a capacitor will reach a certain voltage after a certain amount of time has elapsed.
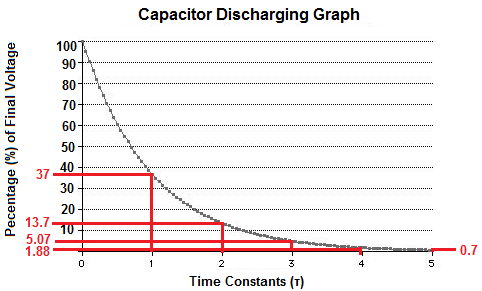
The time it takes for a capacitor to discharge 63% of its fully charged voltage is equal to one time constant. After 2 time constants, the capacitor discharges 86.3% of the supply voltage. After 3 time constants, the capacitor discharges 94.93% of the supply voltage. After 4 time constants, a capacitor discharges 98.12% of the supply voltage. After 5 time constants, the capacitor discharges 99.3% of the supply voltage.
The graph below shows all these transitions of capacitor discharging time:
Related Resources
Capacitor Impedance Calculator
Capacitive Reactance
How to Calculate the Current Through a Capacitor
How to Calculate the Voltage Across a Capacitor