Factoring Calculator

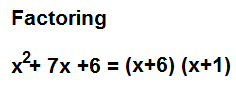
The factoring calculator calculates the factors that comprise a polynomial.
This calculator deals exclusively with binomials and trinomials. It does not calculate the factors of any other type of polynomial.
A binomial is a polynomial that contains 2 terms. Examples of binomials are x2-36, 2x2-40, and x2-100.
A trinomial is a polynomial that contains 3 terms. Examples of trinomials include x2 +3x +2, 2x2-14x-7, and 7x2+5x-14.
This calculator calculates the factor of polynomials of the 2nd degree, meaning the highest exponent x value is of the 2nd degree. It does not go beyond the 2nd degree. Therefore, it does not calculate cubes or exponents above 2.
Other important things to know about this calculator is the variable must be x in the expression. This is the only variable that the calculator recognizes. But this functionality is being worked on to take in any variable.
The expression will always be factored if the expression can be factored, but it may not always be reduced fully. This calculator is a factoring calculator chiefly, not reducer. But this functionality will be worked on.
This calculator is used for electronics because electronics requires a broad amount of mathematics. So factoring equations may be necessary in certain instances.
This factoring calculator calculates the factors that comprise a polynomial via a number of methods.
One common method that is done is that the calculator looks at all the terms in the polynomial.
It's easier to visualize with this with an actual example, so we'll look at an example now.
x2 + 11x + 24
So, in this example, the first term is 1 and the last term is 24. The calculator will multiple these terms together to get the value of 24. This value of 24 is very important because it represents the last term of a polynomial. So once we obtain this value of 24, the calculator then looks at all the factors of 24, which are {1,24}, {2, 12}, {3,8}, and {4,6}. The calculator then looks at the middle term. It sees whether any of the factors add up to the middle term. If any of the factors do, then it's a match. And these are the factors that comprise the polynomial. So in this case, the factors are 3 and 8. So the final answer is (x+3)(x+8).
This is the case if all the values are positive.
Let's now look at an example where the all the numbers are not positive and see how this calculator modifies.
So, we'll use values similar to the polynomial above, but make the last term negative.
x2 -5x - 24
So now the first term is 1 and the last term is -24. These produces a product of -24. Again, we use the factors of 24 which are {1,24}, {2, 12}, {3,8}, and {4,6}. Being that it is negative this implies that one of the terms is negative and the other is positive, since the only way to get a negative is with a positive and negative. So when one factor is negative and the other is positive, the numbers do not add but really subtract. Therefore, when the last term is negative, as in this case, the middle term is the difference of the matched factors. Being that the middle term is -5 in this case, the factors are -8 and 3. So the final answer is (x-8)(x+3).
This is one method that the calculator uses to compute the factors of a polynomial.
However, this method won't catch all the values using this method.
The gold standard method of computing factors is via the quadratic formula computation.
Using the quadratic formula below, we can compute the factors which make up a polynoimal.
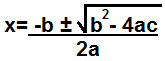
The quadratic formula computes the 2 factors that make up a polynomial.
If the results of the quadratic formula come up as whole numbers, then the polynomial can be factored. If the results come up as fractional numbers, then the polynomial may be able to be factored depending on the value of the coefficient of the first. If the results can neither whole numbers nor fractions, then the polynomial cannot be factored.
An example of a polynomial in which the quadratic formula produces whole numbers is shown below.
x2 + 20x + 21
Solving the quadratic equation gives the factors of x= -1 and x= -20. Both of these factors are whole numbers.
So the final factoring of the polynomial gives the answer of (x+1)(x+20).
An example of a polynomial in which the quadratic formula produces fractional numbers is shown below.
18x2 +54x +28
Solving the quadratic equation gives the factors of x= -2 1/3 and x=-2/3.
But this is not the final answer. Notice how the coefficient in front of the first term is 18. If we break up 18 into the factors 6 and 3, we can multiply these factors by the values obtained in the quadratic formula to produce whole numbers. 6 * -2 1/3= -14, so one factor is -14. 3 * -2/3= -2, so the other factor is -2. This produces the factoring of the polynomial to give the final result of (6x+14) (3x+2).
An example of a polynomial that produces results that are neither whole nor fractional is shown below.
6x2 + 8x +4
The quadratic formula for this equation cannot be solved. Thus, this equation cannot be factored.
This is because when solving for the quadratic formula in the square root, the number is negative. The square root for
a negative number is undefined, so the equation cannot be solved.
So you can see how important the quadratic formula can be and how it is used to find factorings for a polynomial (if factoring is possible).
Therefore, this factoring calculator uses the quadratic formula heavily to make computations to
see whether the polynomial is factorable or not.
Related Resources
