Half Life Calculator

Initial Amount: (optional)

Half Life: hours

Time That Has Passed: hours

Answer:

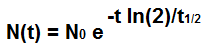
The half life calculator is calculates the remaining amount of a substance based on the half life of the substance and the time that has elapsed.

With this half life calculator, the user has the option of entering in an initial amount or not. If the user doesn't enter in the initial amount of the substance (the amount before the time has transpired), then the calculator will compute the fractional (decimal) portion of the number that remains of the original amount (after the time has transpired). If a user enters in the initial amount of the substance, then the calculator calculates the amount of the substance that remains in the units entered.

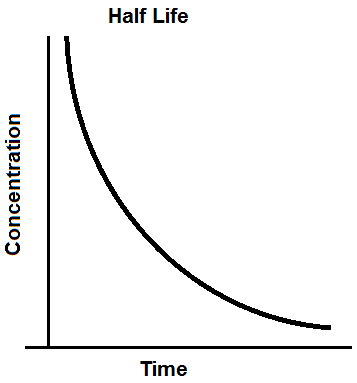
If a user enters in an initial amount, the formula which calculates the half life is, N(t)= N₀e^{-t ln(2)/t_1/2}. N₀ stands for the initial amount of the substance (before the time has elapsed). t stands for the time that has elapsed. t_1/2 stands for the half life of the substance. The formula calculates the remaining amount based on the e function. The e function is raised to a negative value, which means that is exponential decline in value. This is why the half life curve descends in value exponentially as time goes by.

If a user doesn't enter in an initial amount, the formula which calculates the half life is, N(t)= e^{-t ln(2)/t_1/2}. Basically it's the same as the last formula with the exception that the initial amount of the substance, N₀, is removed from the formula.

The half life calculator can be used to calculate the remaining amount of anything such as radioactive decay or for drug calculations. Let's say, for instance, there is a drug that is given in a 10mg dose. It has a half life of 6 hours. This means that 6 hours later, half of the medication will be consumed, leaving half remaining, at 5mg. Then another 6 hours another half will be consumed, leaving 2.5mg remaining in the person's body after 12 hours has transpired. Drugs are notorious for having half lives, because it has to be known how long a drug will stay in the human body. This is necessary so that it can be known how often a person can take dosages of drugs, to avoid building up a toxic drug level in the body. Drugs with longer half lives are at higher risk for abuse and dangerous toxicity levels, because it lasts longer in the body; therefore, if a person keeps taking more and more of it (being that it has a longer half life, it remains in the body longer), dangerous levels of the drug can be built up. So calculating half lives is very important for many reasons, ranging from radioactive materials to drug use.

To use this calculator, a user simply enters in the half life and the time that has transpired. Entering in the initial amount of the substance is optional. Then the user clicks on the 'Calculate' button, and the resultant answer is automatically calculated and shown.

Examples

A 10mg drug has been administered to a patient. It has a half life of 12 hours. 16 hours has transpired. How much of the drug remains?

N(t)= N₀e^{-t ln(2)/t_1/2}= (10)e^{-16 (ln(2))/12}= 3.97mg.

So 3.97mg of the drug remains in the body.

A drug has been administered to a patient which has a half life of 24 hours. 26 hours has transpired. How much of the drug remains?

N(t)= e^{-t ln(2)/t_1/2}= e^{-26 (ln(2))/24}= 0.47

So after 26 hours has transpired, 0.47 of the original amount remains in the person.

Related Resources

Scientific Notation Converter

Parts Per Million (PPM) Calculator

PPM to Percent Calculator

Percent to PPM Calculator