Op Amp Oscillator Calculator
RC Op Amp Oscillator
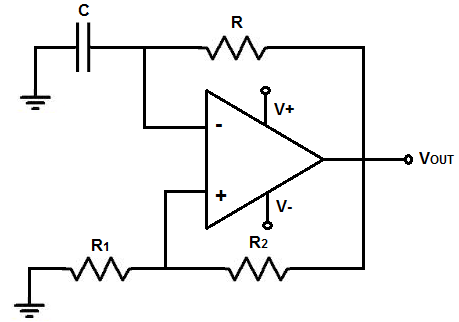

The RC frequency calculator is a calculator that computes the frequency that is created from a resistor and capacitor combined together.
The RC circuit is composed of 1 resistor and 1 capacitor.
With a resistor and capacitor in the same circuit, oscillations are produced. As the capacitor charges up and discharges, charges up and discharges, over and over again, this creates the sinusoidal waveform at the input of the op amp. In turn, there is an oscillatory waveform at the output of the op amp directly in proportion to the RC network.
The frequency of the RC network is determined by the formula, frequency= 1/2πRC, where R is the resistance value and C is the capacitance value.
LC circuits can be incorporated into many different electronic components such as op amps, transistors, logic chips. Regardless of which component it is used in, it serves the same function and its composition of one resistor and one capacitor remains unchanged. Therefore, this calculator can be used for any RC circuit. The formula for calculating the frequency of the RC circuit will remain unchanged.
This calculator uses a variety of resistor and capacitor values. This calculator tries to take into account values of resistors and capacitors that are easy to find for breadboarding purposes. Large capacitor values are usually very hard to find. Components easily obtained for capacitors are values from 1pF to 4700μF. Therefore, this calculator avoids all very large capacitor values and simply uses values in the easy-to-find capacitance range of 1pF to 4700μF.
Resistor values are most commonly used in the ohms to megohms range. Resistors are usually easily accessible regardless of value, because they are such a widely used component. In this calculator, resistor values are kept relatively low from about 100Ω to a few kilohms.
Even though you will not find exact values for breadboarding purposes, there are values close enough that you could find that will make the frequency still very close to the desired frequeny you want to obtain.
In general, low frequencies require large capacitor or resistor values. For very small frequency signals, such as a few hertz in frequency, very large values are needed for either the capacitance or resistance. As the value of the frequency increases, the values of the capacitor and resistor get much smaller. At very high frequencies, such as in the megahertz range, very small capacitor or resistor values are used. For frequencies 1MHz or greater, capacitor values in the picofarads are used.
This calculator can handle frequencies up to a few gigahertz. After this frequency, the resistor values fall too low and are difficult to find, thus making the circuit uneasily accessible to build. But normally circuits don't deal with frequencies nearly so high, so this calculator can give very practical components that are easy to find.
To use this calculator, a user simply has to enter the frequency desired and the gain deisred. If the gain is not important, it does not have to be entered in. The frequency can be entered in hertz (Hz), kilohertz (KHz), and megahertz (MHz). The calculator will then compute the value of the component values of the circuit.
As stated, RC circuits may be built with an op amp, a transistor, or inverter logic chip,
but its composition of an resistor and capacitor is the same for each
case. Therefore, this formula and calculator will work for any arrangement.
LC Op Amp Oscillator
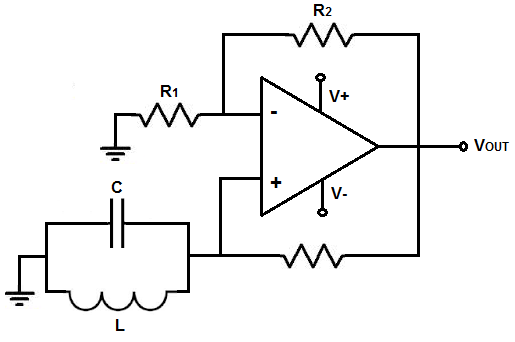

This LC op amp oscillator circuit uses an LC network to create oscillations.
The LC resonance frequency calculator is a calculator that computes the resonant frequency that is created from a single inductor and a single capacitor combined together.
The LC resonant circuit is composed of 1 inductor and 1 capacitor.
Just like an RC circuit, oscillations are produced. RC circuits have a frequency according to the formula, frequency= 1/RC.
LC circuits have a frequency according to the formula, frequency= 1/2πLC.
LC circuits produce oscillations through the continual discharging and recharging of a capacitor.
Just like RC circuits, LC circuits can be incorporated into many different electronic components such as op amps, transistors, logic chips. Regardless of which component it is used in, it serves the same function and its composition of one inductor and one capacitor remains unchanged. Therefore, this calculator can be used for any LC circuit. The formula for calculating the frequency of the LC circuit will remain unchanged.
This calculator uses a variety of inductor and capacitor values. This calculator tries to take into account that for breadboarding purposes, large capacitor values are usually very hard to find. Components easily obtained for capacitors are values from 1pF to 4700μF. Therefore, this calculator only uses large capacitor values (up to 1 farad) for very small frequencies such as from 1Hz to 100Hz. Other than this, large capacitor values are avoided due to the fact of not easy accessibility.
Inductor values are most commonly used in the nanohenries to microhenries range. Just like with capacitors, large values for inductors such as in the millihenry range are generally avoided due to the fact that capacitors in the millifarads range are hard to obtain and not easily accessible. In fact, in this calculator, frequency values only from 1-2Hz utilize inductors in the millihenry range. The rest of inductors are smaller, which is much more easily accessible.
In general, low frequencies require very large capacitor and inductor values. For very small frequency signals, such as a few hertz in frequency, very large values are needed for the inductor and capacitor. As the value of the frequency increases, the values of the capacitors and inductor get much smaller. At very high frequencies, such as in the megahertz range, very small inductor and capacitors values are used. For frequencies 1MHz to 99.99MHz, capacitors in the picofarads range and an inductor in the microhenry range are used. For frequencies 100MHz or greater, capacitors in the picofarads and an inductor in the nanohenries is used.
This calculator can handle frequencies up to a few gigahertz. After this frequency, the inductors values fall too low and inductors so small in value are hard to find, thus making the circuit uneasily accessible to build. But normally circuits don't deal with frequencies nearly so high, so this calculator can give very practical components that are easy to find.
To use this calculator, a user simply has to enter the frequency desired. The frequency can be entered in hertz (Hz), kilohertz (KHz), and megahertz (MHz). The calculator will then compute the value of the inductor and capacitor.
As stated, LC circuits may be built with an op amp, a transistor, or inverter logic chip,
but its composition of an inductor and capacitor is the same for each
case. Therefore, this formula and calculator will work for any arrangement.
Be aware though that although op amps can work totally well as oscillators, there are limits that must be taken into account. It's not all perfect.
One thing that must be taken into account is an op amp's slew rate. The slew rate is the rate at which an op amp can put out voltage per a given unit time. In other words, it's the speed at which the op amp can output voltage.
Op amps with low slew rates can't put out voltage very fast, so at high frequencies, there will be considerable distortion at the output, simply because the op amp can't keep up. Slew rates must be known and taken into account unless dealing with very low frequencies and voltages.
A second specification that must be taken into account is bandwidth limitations. An op amp may not be able to span the entire bandwidth you want it to.
So, although op amps can work well as oscillators, certain criteria such as frequency and voltage levels must be taken into account.
Related Resources
Colpitts Oscillator Calculator
Hartley Oscillator Calculator
7414 Oscillator Calculator
