Power Rule Calculator (for Differentiation)

Enter a function to differentiate with the power rule:



Answer:

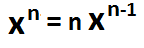
How to Enter in the Function
Enter x^6 = x⁶
Enter 7x^2 = 7x²
Enter y^8= y⁸

This power rule calculator differentiates the function which a user enters in based on the calculus power rule.

The power rule is calculated is illustrated by the formula above.

We will repeat the formula again. It is xⁿ= nx^n-1.

Thus we take the exponent of the base and multiply it by the coefficient in front of the base. We then subtract one from the exponent.

Examples of the power rule in effect are shown below:

x⁶= 6x⁵
x⁸= 8x⁷
x³= 3x²
x⁸= 8x⁷

If there is a coefficient in front of the base, then this coefficient gets multiplied by the value of the exponent. Thus if we have n₁x^n₂= n₁n₂x^n₂-1.

Examples of this include:

7x⁸= 56x⁷
10x⁶= 60x⁵
5x⁹= 45x⁸
3x⁴= 12x³

To use this calculator, enter in the function. If there is no coefficient in front of the base, just enter the base ^ the exponent, such as x^7. If there is a coefficient, simply just enter the coefficient, such as 10x^7. Do not put any multiplication sign in the function. Then just click the 'Differentiate' button and the derivative will be computed and displayed below.

The power rule is just one of many differentiation rules to solve for the derivative of a function. Finding the derivative of functions is crucial to solving many different types of math problems. Many electronics problems utilize differentiation to solve for unknowns, including many electromagnetics problems.

Related Resources

Capacitor Impedance Calculator

Capacitive Reactance

How to Calculate the Current Through a Capacitor

How to Calculate the Voltage Across a Capacitor