Resistance Calculator

Resistance Calculator By Ohm's Law
(if Voltage and Current Are Known)
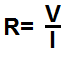
This resistance calculator calculates the resistance of an electronic component based on the voltage which is dropped across the component and the amount of current going through the component, according to the formula, R=V/I.
A user enters the voltage, V, and the current, I, and the result will automatically be calculated and shown. The resistance result which is displayed above is in unit ohms (Ω).
This equation above represents ohm's law.
Resistance Calculator By Power Formula
(if Power and Current/Voltage are Known)

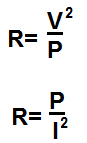
Enter the Power and Voltage or Current to compute result.
This resistance calculator calculates the resistance of an electronic component based on the power that the component consumes and either the voltage which is dropped across it or the current going through it, according to the formulas, R=V2/P (if power and voltage are known) or R=P/I2 (if power and current are known).
To use this calculator, a user enters the power, P, and either the current, I, or the voltage, V, and the result will automatically be calculated and
shown.
The resistance result which is displayed above is in unit ohms (Ω).
Resistance Calculator By Resistivity Formula
(if resistivity, area, and length are Known)
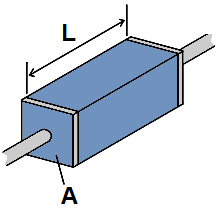
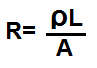
This resistance calculator calculates the resistance of an electronic component from the resistivity formula. The resultant value is based on the resistivity of the wire or material, the length of the wire, and the cross-sectional area of the wire, according to the formula R=ρL/A.
To use this calculator, a user must enter all fields, the resistivity, ρ, of the material, the length, L, of the material, and the cross-sectional area, A, of the material, and the result will automatically be calculated and shown. The resistance result which is displayed above is in unit ohms (Ω).
The resistance of a material is directly affected by its length. The longer a material is, the greater its resistance. And conversely, the shorter a material is, the lower its resistance. This is because in a long material, the electrons must go through more of the material. As they go through more of the material, they must meet up with more or greater resistance. When going through a shorter length material, they meet up with less resistance, since there is less of of the material. As far as the area, resistance is inversely affected by the cross-sectional area of a material. The greater the cross-sectional area, the lower the resistance. And conversely, the lower the cross-sectional area, the higher the resistance. This is because if a material has a greater cross-sectional area, it has more space to allow electrons to pass through without much collision or friction, since the area is larger for electrons to pass. This equals less resistance in the wire and, thus, less resistivity. If the cross-sectional area is very small, this gives much less space for electrons to pass through and they bump and collide into each other, with much friction. This creates greater resistance. The resistance also is affected by the resistivity of the material, which is the amount of resistance a material intrinsically has based on its composition. The greater the resistivity of an element, the more resistance it will offer in a circuit. The lower the resistivity, the less resistance it will offer. Different materials offer many different values of resistivity. Conductors, which are materials that conduct electrons well, have low resistivity values. They don't offer much resistance in a circuit and allow for free movement of electrons. Insulators, on the other hand, have very high resistivity values. This is because insulators do not allow for easy movement of electrons through them. They oppose the flow of electrons. A material with a high resistivity value, or an insulator, offers much greater resistance. As an example, copper, a great conductor, has a resistivity of 1.68 x 10-8. Meanwhile, hard rubber, an insulator, on the other hand, has a resistivity value of 1 x 1013. Thus, if all other factors are kept the same, hard rubber will offer much greater resistance in a circuit than copper.
A tip to use this calculator is when entering the resistivity value, use the e function to enter this value. For example, if entering the resistivity value of copper, which again is, 1.68 x 10-8, enter in 1.68e-7.
For reference, below is a chart of common resistivities of various
elements represented at 20°C. Since resistivity is temperature dependent, it changes
for various temperatures. Therfore,
when listing resistivity, it must be stated at a specific temperature:
Table of Resistivity of Materials
| Material |
(ohm • m) |
|
| Silver |
|
|
| Copper |
|
|
| Aluminum |
|
|
| Tungsten |
|
|
| Iron |
|
|
| Platinum |
|
|
| Manganin |
|
|
| Lead |
|
|
| Mercury |
|
|
| Nichrome |
|
|
| Carbon |
|
|
| Glass |
|
|
| Hard rubber |
|
|
Related Resources
Parallel and Series Resistor Calculator
Resistivity Calculator
Thermal Resistance Calculator
Capacitor Impedance Calculator