Superposition theorem
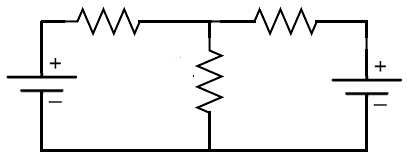
In this article, we explain the superposition theorem.
The superposition theorem is used in circuits that have mutiple power sources (2 or more power sources).
According to the superposition theorem, we can analyze a circuit one power source at a time. This allows for easier analysis than when considering all of the power sources all at once. We then can add up all the currents or voltages to get the total current or voltage in a certain part of the circuit.
When applying the superposition theorem, voltage sources are shorted out and current sources are replaced with an open circuit.
So this is how a circuit is analyzed with the superposition.
The circuit is analyzed with one power source in it and the remaining voltage sources shorted out and the current sources replaced with an open circuit.
At the end, once we have analyzed the circuit from each power source separately (with that one power source in the circuit and the other removed), we add up all the currents and voltages in each part of the circuit and this will equal the total current and voltage (in that part of the circuit).
So the best way to see the superposition theorem in practice is do an example. So we will
do one now.
Superposition Practice Problem
So now we'll analyze the circuit below with 2 power sources (voltage sources).
Applying the superposition theorem, we can find the currents and voltages in each part of the circuit.
We analyze the circuit one power source at a time and then add the values at the end to get the total current and voltage values.
The brilliance of the superposition theorem is that it simplifies the circuit. Analyzing a circuit with multiple power sources present is difficult and can be very confusing.
Superposition allows us to do circuit analysis one circuit at a time.
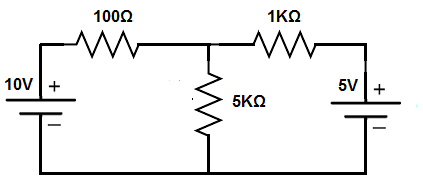
So the above circuit is the circuit we will analyze using the superposition theorem.
We will first analyze the 10V DC power source. Therefore, the 5V DC power source is removed.
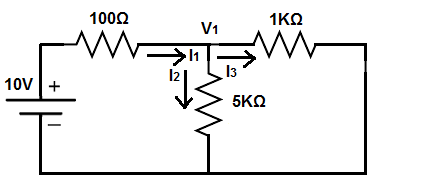
So, above, is how the circuit will look when the 5V power source is removed.
With one power source, it is now simpler to analyze.
Notice how the 1KΩ resistor and the 5KΩ resistor are in parallel. Therefore, we can can take the resistance of these 2 components by the formula, R2 || R3 = (1KΩ)(5KΩ)/(1KΩ+5KΩ)= 833Ω.
This 833Ω is now in series with the 100Ω resistor, which gives a total resistance of 933Ω.
We can now figure out the total current produced by the power supply (I1), which is, 10V/(933Ω)= 10.7mA.
We now can figure out the currents I2 and I3 by current division.
The formula for current division is, IS(RT/RX, where IS is the total current flow (or source current flow) before the current is divided up, RT is the total resistance of all of the branches of the circuit where the current will be divided to, and RX is the resistance of the specific branch that you want to calculate the current flow to.
The current of I2 is, (10.7mA)(833Ω/5KΩ)= 1.78mA.
Therefore, the current of I3 is, (10.7mA)(833Ω/1KΩ)= 8.9mA.
Adding 8.91mA and 1.78mA gives us the original 10.7mA.
Now that we know the currents we can figure out the voltage with ohm's law, with the formula, voltage= current * resistance (V=IR).
The voltage drop across the 100Ω resistor is, (10.7mA)(100Ω)= 1.1V.
The voltage drop across the 5KΩ resistor is, (1.78mA)(5KΩ)= 8.9V.
The voltage drop across the 1KΩ resistor is, (8.9mA)(1KΩ)= 8.9V. You could also tell the voltage across the 1KΩ resistor would be the same as across the 5KΩ resistor, since they are both in parallel with each other.
So we have calculated all currents and voltages with the 10V DC power suppply.
We will now analyze the circuit to calculate the currents and voltages through the
5V DC power supply.
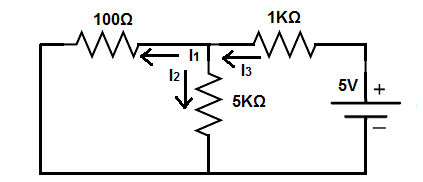
We now do the same thing with this circuit.
The 100Ω and the 5KΩ resistor are in parallel with each other. The formula for calculating the equivalent resistance of these 2 resistors is, R1 || R2= (100Ω)(5KΩ)/(100Ω + 5KΩ)= 98Ω.
The 98Ω total resistance is now in series with the 1KΩ resistor, which gives a total resistance of 1098Ω.
With this we can now calculate the total current (I3), which gives us, I3= 5V/1098Ω= 4.6mA.
We then use the current division formula to calculate currents I2 and I1.
I2= 4.6mA(98Ω/5KΩ)= .09mA.
I1= 4.6mA(98Ω/100Ω)= 4.5mA.
We can calculate the voltages using ohm's law.
The voltage drop across the 1KΩ resistor is, (4.6mA)(1KΩ)= 4.6V.
The voltage drop across the 5KΩ resistor is, (0.09mA)(5KΩ)= 0.45V.
The voltage drop across the 100Ω resistor is, (4.5mA)(100Ω)= 0.45V. You can know this by the fact that the 5KΩ resistor and the 100Ω resistor are in parallel.
Now we have all the voltages and currents based on both analyses.
So, going back to the original circuit, the current going through the 100Ω resistor is, 10.7mA + (-4.51mA)= 6.52mA (going away from the 10V power source). The currents subtract because they are in opposite directions.
The current going through the 5KΩ resistor is, 1.78mA + 0.09mA= 1.87mA. The currents add because the currents from both power supplies go in the same direction.
The current going through the 1KΩ resistor is, 8.9mA + (-4.6mA)= 4.3mA (going toward the 5V power source). They subtract because the currents are in opposite directions.
The voltage drop across the 100Ω resistor is, 0.11V + (-0.45V)= -0.34V.
The voltage drop across the 5KΩ resistor is, 8.9V + 0.45V= 9.35V.
The voltage drop across the 1KΩ resistor is,
8.9V + (-4.6V)= 4.3V.
Superposition Theorem Second Practice Problem with a Current Source
Now we've gone over a problem with the superposition theorem with voltage sources.
Now we will go over how to use the superposition theorem in a circuit with a current source.
Remember that voltage sources are shorted out, while current sources are replaced with an open circuit when using the superposition theorem.
We'll use these principles in the circuit shown below.
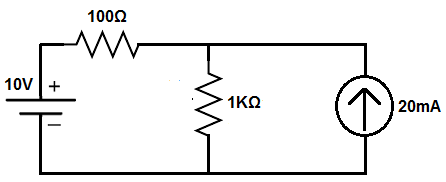
So this circuit above has a voltage source and a current source.
We will first analyze the circuit with the current source removed.
The circuit will look like that which is shown below.
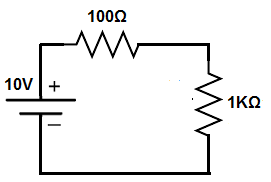
So this is the circuit with the current source removed. The current source was replaced with an open circuit.
This simply leaves the voltage source along with the 2 resistors.
The 2 resistors are in series so the same current flows through each of the 2 resistors. The current flowing through can be calculated according to ohm's law, I= V/R= 10V/(1KΩ + 100Ω)= 10V/1.1KΩ= 9.1mA.
Calculating the voltage drop across the 100Ω resistor is calculated through ohm's law, V=IR= (9.1mA)(100Ω)= 0.91V.
The voltage drop across the 1KΩ resistor is, V=IR=(9.1mA)(1KΩ)= 9.1V.
Now let's analyze the circuit through the current source (with the voltage source removed).
The circuit will look like that shown below.
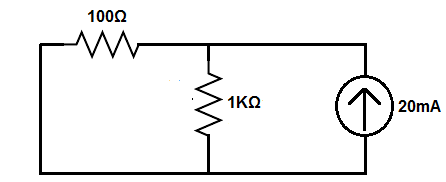
So with this current source, which is 20mA, we have a current divider circuit. The 20mA current divides up into the 100Ω and the 1KΩ resistors.
Using the current divider formula, we calculate the current through the 1KΩ resistor to be, IS(RT/RX)= 20mA(91Ω/1KΩ)= 1.82mA. The equivalent resistance, RT, is calculated through the formula 100Ω || 1KΩ.
The current through the 100Ω resistor is, IS(RT/RX)= 20mA(91Ω/100Ω)= 1.82Ω= 18.2mA.
The voltage across the 100Ω resistor is, V=IR= (18.2mA)(100Ω)= 1.82V.
The voltage across the 1KΩ resistor is, V=IR= (1.82mA)(1KΩ)= 1.82V.
The voltage across the 100Ω resistor and the 1KΩ resistor are the same, being that they are in parallel with each other.
Now we can add up all the voltages and currents to get the total voltages and currents in each part of the circuit.
The current flowing through the 100Ω resistor is, 9.1mA + (-18.2mA)= -9.1mA, which means that current is flowing toward the voltage source.
The current flowing through the 1KΩ resistor is, 9.1mA + 1.82mA= 10.92mA.
The current flowing through the branch containing the current source is 20mA flowing away from the current source. This is because we are examining the current source as if it's an ideal current source; therefore, the current source has infinite internal resistance. Because of this infinite internal resistance, no current flowing from the voltage source goes to the branch of the circuit containing the current source. All of it instead flows through the 1KΩ resistor.
The voltage across the 100Ω resistor is, 0.91V - (1.82V) = -0.91V.
The voltage across the 1KΩ resistor is, 9.1V + 1.82V= 10.92V.
And because the current source is in parallel to the 1KΩ resistor, it has the same voltage drop across it.
So this is how superposition works. It's a very valuable tool, because it allows us to analyze circuits that have multiple power sources,
analyzing the circuit with one power source at a time.
It allows us to simplify circuits so that we can calculate voltages and currents easier.
Related Resources
Kirchhoff's Voltage Law
What is an Ideal Current Source?
What is a Constant Current Source?
RMS Voltage and Current- Explained
