Ideal Current Source Explained

An ideal current source is a current source that supplies constant current to a circuit despite any other conditions present in the circuit.
An ideal current source provides this constant current with 100% efficiency. Thus, if an ideal current source is a 12mA current source, the load will receive the entire 12mA, without any being lost.
Unlike an ideal voltage source that has zero internal resistance, an ideal current source has infinite internal resistance;
this allows it to act as a 100% efficient source of current.
Why Does an Ideal Current Source Have Infinite Internal Resistance?
The reason why an ideal current source has infinite internal resistance will now be explained.
Before we do that, realize that the job of a power source, whether voltage or current, is to supply power to a load in a circuit, so that a load can be turned on and, thus, operate. So, we want to ideally supply 100% of the power from the power source to the load. This is power transfer. In order to supply 100% of the power from the source to the load, we must allocate the resistances in the circuit appropriately so that the load receives this power. This is called current division. Current always takes the path of least resistance. Thus, in order for current to go to the path of least resistance, we must set up the source and load so that the source has much higher resistance than the load. This will ensure that the current travels from source to load. This is why we construct the ideal current source to have infinite internal resistance. This will ensure that current will flow out of it and take the path of least resistance, which will be the load, since the load will not have infinite internal resistance.
When the current source has infinite internal resistance, the output current from the source will not change despite changes in resistance value from the load. The current will
always want to escape out of its infinite resistance to a lower resistance. This produces a current output graph below of an ideal current source:
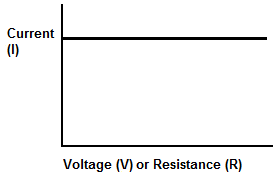
Since the internal resistance of the current source is infinite, any changes in resistance value of the load have no effect on changing the steady current value. The infinite resistance is dominant and causes no current change despite fluctuations in load resistance.
Let's examine a circuit with an ideal current source, shown below:
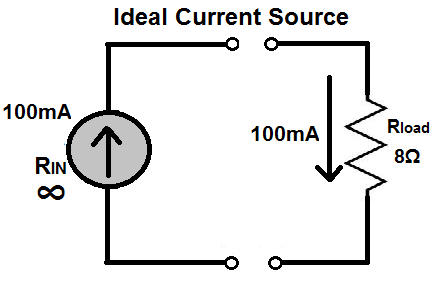
Because the current source has infinite impedance, the current from the source looks to escape and go to through a path of lesser resistance, which is the 8Ω load. All of the current from the current source (100mA) flows through the 8Ω resistor load. This is the ideal case and is 100% power efficiency.
Now let's examine the circuit with a real current source, shown below:
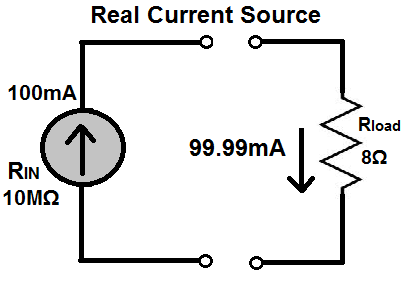
This current source has 10MΩ of resistance, which is high enough to give a very close current to the full value of the current source, 100mA; however, the current source will not give 100% of its power. This is because the internal resistance of the current source will still eat up some of the current and lead to current waste. This can be calculated using current division. The source gives out 100mA. Current then is divided up between the 10MΩ load and the 8Ω load. The formula to calculate how much current goes through the 8Ω load is I= (100mA)(10MΩ/10MΩ+8Ω)= 99.9999mA.
Though ideal current sources do not exist, they serve as a model so that we can construct real current sources that mimic as close as possible the characteristics of an ideal
current source.
Related Resources
How to Build a Current Source Circuit
What is an Ideal Voltage Source?
Kirchhoff's Voltage Law (KVL)
Kirchhoff's Current Law (KCL)
