Calcolatrice Fattorizzazione


Il calcolatore fattorizzazione calcola i fattori che compongono un polinomio.
Questa calcolatrice si occupa esclusivamente di binomi e trinomi. Esso non calcola i fattori di qualsiasi altro tipo di polinomiale.
Un binomio è un polinomio che contiene 2 termini. Esempi di binomi sono x2-36, 2x2-40, e x2-100.
Un trinomio è un polinomio che contiene 3 termini. Esempi di trinomi includono x2+3x+2, 2x2-14x-7, e 72+5x-14.
Questa calcolatrice calcola il fattore di polinomi di 2 gradi, il che significa il più alto valore dell'esponente x è di 2 gradi. Esso non va oltre il 2 gradi. Pertanto, esso non calcola cubi o esponenti di sopra del 2.
Altre cose importanti da sapere su questa calcolatrice è la variabile deve essere x nell'espressione. Questa è l'unica variabile che la calcolatrice riconosce. Ma questa funzionalità è in lavorazione a prendere in qualsiasi variabile.
L'espressione sarà sempre scomposto se l'espressione può essere preso in considerazione, ma non può sempre essere ridotto completamente. Questo calcolatore è un calcolatore di fattorizzazione soprattutto, non riduttore. Ma questa funzionalità sarà lavorato.
Questo calcolatore fattorizzazione calcola i fattori che compongono un polinomio tramite un certo numero di metodi.
Un metodo comune che si fa è che la calcolatrice esamina tutti i termini del polinomio.
E 'più facile da visualizzare con questo con un esempio reale, quindi dovremo guardare un esempio ora.
x2 + 11x + 24
Quindi, in questo esempio, il primo termine è 1 e l'ultimo termine è 24. La calcolatrice multipli questi termini insieme per ottenere il valore di 24. Questo valore di 24 è molto importante perché rappresenta l'ultimo termine di un polinomio. Quindi, una volta che si ottiene questo valore di 24, il calcolatore poi guarda tutti i fattori di 24, che sono {1,24}, {2, 12}, {3,8} e {4,6}. La calcolatrice poi guarda il termine medio. Si vede se uno qualsiasi dei fattori di aggiungere fino a medio termine. Se uno qualsiasi dei fattori di fare, allora si tratta di una partita. E questi sono i fattori che compongono il polinomio. Quindi, in questo caso, i fattori sono 3 e 8. Quindi la risposta finale è (x + 3) (x + 8).
Questo è il caso se tutti i valori sono positivi.
Diamo ora un'occhiata a un esempio in cui i tutti i numeri non sono positivi e vedere come questa calcolatrice modifica.
Quindi, useremo valori simili a polinomio sopra, ma facciamo l'ultimo termine negativo.
x2 -5x - 24
Così, ora il primo termine è 1 e l'ultimo termine è -24. Questi produce un prodotto di -24. Anche in questo caso, usiamo i fattori di 24 che sono {1,24}, {2, 12}, {3,8} e {4,6}. Essendo che è negativo questo implica che uno dei termini è negativo e l'altro è positivo, poiché l'unico modo per ottenere un negativo è con una positiva e negativa. Così, quando un fattore è negativo e l'altro è positivo, i numeri non ma davvero sottraggono. Pertanto, quando l'ultimo termine è negativo, come in questo caso, il termine medio è la differenza dei fattori corrispondenti. Essendo che il termine medio è di -5 in questo caso, i fattori sono -8 e 3. Quindi la risposta finale è (x-8) (x + 3).
Questo è un metodo che utilizza la calcolatrice per calcolare i fattori di un polinomio.
Tuttavia, questo metodo non prendere tutti i valori usando questo metodo.
Un potente metodo di fattori di calcolo avviene tramite il calcolo della formula quadratica.
Utilizzando la formula quadratica seguito, possiamo calcolare i fattori che compongono un polinomio.
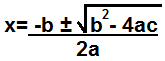
La formula quadratica calcola i 2 fattori che compongono un polinomio.
Se i risultati della formula quadratica venire come numeri interi, quindi il polinomio può essere scomposto. Se i risultati vengono come numeri frazionari, allora il polinomio può essere in grado di essere presi in funzione del valore del coefficiente del primo. Se i risultati non possono né numeri interi né frazioni, allora il polinomio non possono essere presi.
Un esempio di un polinomio in cui la formula quadratica produce numeri interi è mostrato sotto.
x2 + 20x + 21
Risolvendo l'equazione quadratica dà i fattori di X = -1 e x = -20. Entrambi questi fattori sono numeri interi.
Così la fattorizzazione finale del polinomio dà la risposta di (x + 1) (x + 20).
Un esempio di un polinomio in cui la formula quadratica produce numeri frazionari è mostrato sotto.
18x2 +54x +28
Risolvendo l'equazione quadratica dà i fattori di x = -2 1/3 e x = -2 / 3.
Ma questa non è la risposta finale. Si noti come il coefficiente di fronte al primo termine è 18. Se suddividiamo 18 sui fattori 6 e 3, possiamo moltiplicare questi fattori dai valori ottenuti nella formula quadratica per produrre numeri interi. 6 * -2 1/3 = -14, quindi un fattore è -14. 3 * -2 / 3 = -2, così l'altro fattore è -2. Questo produce la fattorizzazione del polinomio per dare il risultato finale (6x + 14) (3x + 2).
Un esempio di un polinomio che produce risultati che non sono né insieme né frazionaria è mostrato sotto.
6x2 + 8x +4
La formula quadratica per questa equazione non può essere
risolto. Così, questa equazione non può essere scomposto.
Questo perché quando risolvendo la formula quadratica nella radice quadrata,
il numero è negativo. La radice quadrata di un numero negativo è indefinito,
quindi l'equazione non può essere risolto.
Così si può vedere quanto sia importante la formula quadratica può essere e come viene utilizzato per trovare la fattorizzazione per un polinomio (se la fattorizzazione è possibile).
Pertanto, questo calcolatore fattorizzazione utilizza la formula quadratica
pesantemente fare calcoli per vedere se il polinomio è factorable o meno.
Risorse Correlate
Calcolatrice di Notazione Scientifica
Calcolatrice dell'Intervallo di Confidenza
