Calculadora de Cifras Significativas

Esta Calculadora de cifras significativas calcula el número de cifras significativas que contiene un número y muestra las cifras que son significativas.
Las cifras significativas son los valores en un número que se puede contar para ser exactos. Las cifras significativas en un número son aquellos valores que se pueden conocer con certeza o un alto grado de confianza, mientras que los dígitos insignificantes son aquellos en los que no confiamos como muy precisos.
Las cifras significativas se utilizan ampliamente durante las mediciones. Diferentes herramientas de medición pueden registrar medidas de diferente precisión. Algunas herramientas de medición pueden registrar mucho más en detalle que otras herramientas de medición. Por ejemplo, si tenemos una regla que sólo mide centímetros, podemos medir hasta un centésimo de metro. Si ahora cambiamos la regla y obtenemos una que ahora mide milímetros, podemos medir a una milésima de metro. Por lo tanto, podemos tener un dígito extra significativo, porque la regla es más detallada y permite una mayor precisión de la medición.
Es importante ser honesto al realizar una medición, de modo que el valor resultante no parece ser más preciso que el equipo utilizado para hacer la medición lo permite. Y cómo hacemos que el valor registrado sea honesto es controlando el número de dígitos, o cifras significativas, usados para reportar la medición. El valor registrado no puede tener dígitos más significativos que los permitidos por la herramienta de medición.
Así, por ejemplo, si tomamos una medida y podemos afirmar que el valor es 230 gramos. El 2 y 3 son cifras significativas, mientras que el 0 no lo es. El 0 es incierto porque no confiamos en que sea exacta. Por lo tanto, para el número 230, sólo el 2 y 3 sabemos con un alto grado de precisión, mientras que el 0 es incierto y poco confiable, por así decirlo. Así, el número 230 sólo tiene 2 cifras significativas.
Por ejemplo, una escala de franqueo mide en gramos. No puede medir una décima de un gramo, un centésimo de un gramo, etc, sólo en gramos. Toma una medida en gramos +/- 1 gramo. Por lo tanto, sólo puede medir a la precisión de 1 dígito significativo. Un balance de dos paneles, sin embargo, puede medir a un centésimo de un gramo. Por lo tanto, tendrá 3 cifras significativas, una para los lugares, una para la décima y otra para la centésima. Una balanza analítica puede medir hasta un milésimo de gramo, por lo que puede tener hasta 4 cifras significativas.
Sin embargo, con todas estas herramientas de medición discutidas anteriormente, los dígitos significativos apropiados deben ser respetados. Imagínese si un dispositivo de medición sólo puede medir a un centésimo de un gramo como el equilibrio de dos paneles y decimos que registra una medida a una milésima de un gramo. Esto haría que nuestros resultados fueran muy sospechosos y sería inexacto. Si un dispositivo sólo puede medir a un centésimo de un gramo, ¿cómo puede obtener un valor para ser tan preciso como a una milésima de un gramo. Por lo tanto, cifras significativas pueden ser muy importantes en la comunidad científica. Muestra cuán exacto es un número, basado en el número de dígitos significativos presentes en el número.
Ahora que usted sabe la importancia de las cifras significativas, vamos a repasar las reglas para decidir qué dígitos en un número son significativos y cuáles son insignificantes.
Reglas
∙ Todas las cifras no nulas son significativas.
Ex. 5,4789- Todos los dígitos de son distintos de cero. Por lo tanto, todas las cifras son significativas. Así, tiene 5 cifras significativas.
∙ Los ceros situados entre cifras diferentes de cero son significativos.
Ex. 2,00008- Todos los ceros en este número son significativos. Por lo tanto, tiene 6 dígitos significativos.
∙ Los ceros al final de un número son significativos si el número contiene un decimal.
Ex. 45,00- Los ceros en este número son significativos. Por lo tanto, tiene 4 dígitos significativos.
∙ Los ceros al final de un número son significativos si hay un punto decimal en su lugar.
Ex. 12000,- Los ceros en este número son significativos. Por lo tanto, tiene 5 dígitos significativos.
∙ Los ceros al final de un número son insignificantes si el número no contiene un punto decimal.
Ex. 3.400- Los ceros al final de un número son insignificantes y el número no contienen un punto decimal.
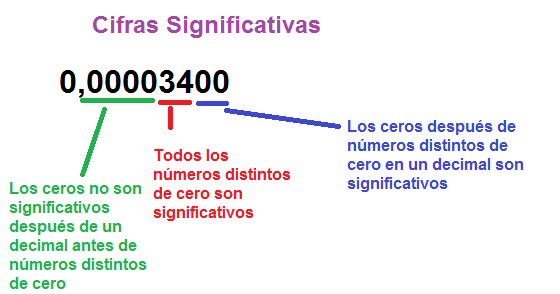
∙ Los ceros a la izquierda del primer dígito distinto de cero después de un punto decimal no son significativos.
Ex. 0,000076- Los ceros en este número no son significativos. Por lo tanto, tiene 2 dígitos significativos.
∙ Los ceros después del primer dígito distinto de cero después de un punto decimal son significativos.
Ex. 0,0005600-Los primeros 3 ceros no son significativos. Los 2 últimos ceros son. Por lo tanto, este número tiene 4 dígitos significativos.
Estas son las reglas generales para saber qué dígitos son significativos y cuáles no.
Para utilizar esta calculadora, un usuario simplemente introduce un número para el cual desea encontrar el número de cifras significativas en el número y los dígitos del número son significativos. Una vez introducido el número, el usuario hace clic en el botón "Buscar Número de Cifras Significativas". Las cifras significativas resultantes se computarán automáticamente.
Siendo que la electrónica, como cualquier otra ciencia, se ocupa de las mediciones, es importante saber cómo tratar con cifras significativas. Dependiendo de la herramienta de medición en uso determina la precisión que puede medir. El uso del número adecuado de cifras significativas puede ser extremadamente importante, por las razones expuestas anteriormente.
Recursos Relacionados
Calculadora de Redondeo de Cifras Significativas
Calculadora de la Suma de Cifras Significativas
Calculadora de la Resta de Cifras Significativas
Calculadora de la Multiplicación de Cifras Significativas
Calculadora de la División de Cifras Significativas
