Tabla de Distribución T
Distribución T de Lado Derecho
Tabla de Distribución T de Lado Derecho
| df/p | 0,40 | 0,25 | 0,10 | 0,05 | 0,025 | 0,01 | 0,005 | 0,0005 |
| 1 | 0,324920 | 1,000000 | 3,077684 | 6,313752 | 12,70620 | 31,82052 | 63,65674 | 636,6192 |
| 2 | 0,288675 | 0,816497 | 1,885618 | 2,919986 | 4,30265 | 6,96456 | 9,92484 | 31,5991 |
| 3 | 0,276671 | 0,764892 | 1,637744 | 2,353363 | 3,18245 | 4,54070 | 5,84091 | 12,9240 |
| 4 | 0,270722 | 0,740697 | 1,533206 | 2,131847 | 2,77645 | 3,74695 | 4,60409 | 8,6103 |
| 5 | 0,267181 | 0,726687 | 1,475884 | 2,015048 | 2,57058 | 3,36493 | 4,03214 | 6,8688 |
| 6 | 0,264835 | 0,717558 | 1,439756 | 1,943180 | 2,44691 | 3,14267 | 3,70743 | 5,9588 |
| 7 | 0,263167 | 0,711142 | 1,414924 | 1,894579 | 2,36462 | 2,99795 | 3,49948 | 5,4079 |
| 8 | 0,261921 | 0,706387 | 1,396815 | 1,859548 | 2,30600 | 2,89646 | 3,35539 | 5,0413 |
| 9 | 0,260955 | 0,702722 | 1,383029 | 1,833113 | 2,26216 | 2,82144 | 3,24984 | 4,7809 |
| 10 | 0,260185 | 0,699812 | 1,372184 | 1,812461 | 2,22814 | 2,76377 | 3,16927 | 4,5869 |
| 11 | 0,259556 | 0,697445 | 1,363430 | 1,795885 | 2,20099 | 2,71808 | 3,10581 | 4,4370 |
| 12 | 0,259033 | 0,695483 | 1,356217 | 1,782288 | 2,17881 | 2,68100 | 3,05454 | 4,3178 |
| 13 | 0,258591 | 0,693829 | 1,350171 | 1,770933 | 2,16037 | 2,65031 | 3,01228 | 4,2208 |
| 14 | 0,258213 | 0,692417 | 1,345030 | 1,761310 | 2,14479 | 2,62449 | 2,97684 | 4,1405 |
| 15 | 0,257885 | 0,691197 | 1,340606 | 1,753050 | 2,13145 | 2,60248 | 2,94671 | 4,0728 |
| 16 | 0,257599 | 0,690132 | 1,336757 | 1,745884 | 2,11991 | 2,58349 | 2,92078 | 4,0150 |
| 17 | 0,257347 | 0,689195 | 1,333379 | 1,739607 | 2,10982 | 2,56693 | 2,89823 | 3,9651 |
| 18 | 0,257123 | 0,688364 | 1,330391 | 1,734064 | 2,10092 | 2,55238 | 2,87844 | 3,9216 |
| 19 | 0,256923 | 0,687621 | 1,327728 | 1,729133 | 2,09302 | 2,53948 | 2,86093 | 3,8834 |
| 20 | 0,256743 | 0,686954 | 1,325341 | 1,724718 | 2,08596 | 2,52798 | 2,84534 | 3,8495 |
| 21 | 0,256580 | 0,686352 | 1,323188 | 1,720743 | 2,07961 | 2,51765 | 2,83136 | 3,8193 |
| 22 | 0,256432 | 0,685805 | 1,321237 | 1,717144 | 2,07387 | 2,50832 | 2,81876 | 3,7921 |
| 23 | 0,256297 | 0,685306 | 1,319460 | 1,713872 | 2,06866 | 2,49987 | 2,80734 | 3,7676 |
| 24 | 0,256173 | 0,684850 | 1,317836 | 1,710882 | 2,06390 | 2,49216 | 2,79694 | 3,7454 |
| 25 | 0,256060 | 0,684430 | 1,316345 | 1,708141 | 2,05954 | 2,48511 | 2,78744 | 3,7251 |
| 26 | 0,255955 | 0,684043 | 1,314972 | 1,705618 | 2,05553 | 2,47863 | 2,77871 | 3,7066 |
| 27 | 0,255858 | 0,683685 | 1,313703 | 1,703288 | 2,05183 | 2,47266 | 2,77068 | 3,6896 |
| 28 | 0,255768 | 0,683353 | 1,312527 | 1,701131 | 2,04841 | 2,46714 | 2,76326 | 3,6739 |
| 29 | 0,255684 | 0,683044 | 1,311434 | 1,699127 | 2,04523 | 2,46202 | 2,75639 | 3,6594 |
| 30 | 0,255605 | 0,682756 | 1,310415 | 1,697261 | 2,04227 | 2,45726 | 2,75000 | 3,6460 |
| ∞ | 0,253347 | 0,674490 | 1,281552 | 1,644854 | 1,95996 | 2,32635 | 2,57583 | 3,2905 |
Para ver esta tabla arriba como una imagen, vea el siguiente enlace: Tabla de Distribución T.
Existen muchas distribuciones diferentes en las estadísticas, y una distribución de uso común es la distribución t.
Las distribuciones T (de student) se usan comúnmente para encontrar el valor t para un conjunto de datos dado, basado en el tamaño de la muestra del conjunto de datos y el nivel de significación. Este valor t puede entonces ser usado para diversos ajustes de estadística, incluyendo intervalos de confianza y pruebas de hipótesis.
Como antecedente, la distribución normal es la clásica y bien conocida distribución en forma de campana. Se centra alrededor de la media del conjunto de datos y tiene un área de 1 por debajo.
La distribución t es similar a la distribución normal en que tiene una forma de curva de campana y tiene un área de 1 por debajo. Al igual que la distribución estándar normal, se centra alrededor de la media, pero su desviación estándar es proporcionalmente mayor en comparación con la distribución Z (normal). Así que la distribución t es más estirada que la distribución Z.
Al igual que con las distribuciones Z, hay una familia entera de diferentes distribuciones t. Cada familia diferente de la distribución t está determinada por los grados de libertad del conjunto de datos. Los grados de libertad (df) del conjunto de datos están determinados por el tamaño de la muestra. Los grados de libertad (df) se calculan mediante la fórmula, df = n-1. Así por ejemplo, si el tamaño de la muestra es 15, los grados de libertad serán, df = (n-1) = (15-1) = 14.
Los tamaños de muestra más pequeños tienen distribuciones t de distorsión más planas y más estiradas que tamaños de muestra más grandes. A medida que estos tamaños de muestra se hacen más grandes, las distribuciones t son menos estiradas y son más altas, acercándose a los valores de la distribución estándar normal. El punto en el que la distribución t es similar a la distribución z está alrededor del punto donde los grados de libertad son 30.
Así que en el gráfico de distribución t, los datos de fila son los grados de libertad, que va de 1 a 30 y luego tiene una fila de ∞, donde los valores están más o menos en línea con la distribución Z.
Las columnas de la distribución t muestran el nivel de significación. Al ir de izquierda a derecha, el nivel de significación se vuelve más y más preciso. Usando el gráfico de distribución t arriba, a la derecha hay un nivel de significancia de 0.40. Este es un nivel de confianza del 60%. La siguiente columna es un nivel de signficance de 0.25 (o 75% de nivel de confianza). La siguiente columna es 0.10 (o nivel de confianza del 90%). La siguiente columna es 0,05 (o nivel de confianza del 95%). La siguiente columna es 0,025 (o 97,5%). La siguiente columna es 0,01 (o un nivel de confianza del 99%). La siguiente columna es 0,005 (o un nivel de confianza del 99,5%). La siguiente columna es 0,0005 (o un nivel de confianza del 99,95%).
Así que para obtener el valor t de un conjunto de datos, todo lo que tenemos que saber son los grados de libertad, el nivel de significación y el método de prueba de hipótesis (una cola o dos colas).
Por ejemplo, supongamos que tenemos el siguiente conjunto de datos: un tamaño de muestra de 20, un nivel de significancia de 0,10 y una prueba de hipótesis de una cola (cola derecha). ¿Cuál es el valor t?
Haciendo las matemáticas, el tamaño de la muestra es 20, por lo que los grados de libertad son, df = (n-1) = (20-1) = 19. Buscando el valor t para un df = 19 y α = 0,10, obtenemos un valor t de 1.327728.
Para las pruebas de hipótesis de dos colas, este valor sería diferente. Esto es porque la prueba de hipótesis de dos colas tiene 2 lados, la cola izquierda y la cola derecha.
Esto se muestra en el siguiente diagrama.
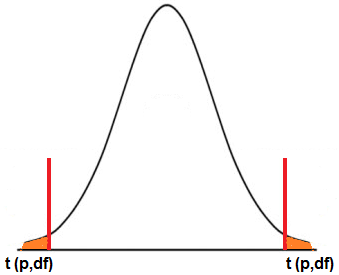
Por lo tanto, con los mismos datos de ejemplo que los anteriores, si usamos pruebas de hipótesis de dos colas y estamos trabajando con el mismo nivel de significancia de 0,10, nuestro nivel de significancia es realmente 0,05 (desde 0,10 / 2 = 0,05). El nivel de significación en la cola izquierda será 0.05 y el nivel de significación en la cola derecha será 0.05. Estos dos agregados dan 0,10.
Por lo tanto, cuando está haciendo pruebas de hipótesis de dos colas con la distribución t, que puede utilizar si el tamaño de la muestra es inferior a 30 para un conjunto de datos, entonces quiere tomar el nivel de significación y dividirlo por 2. Es esto dividido número que se utiliza como el nivel de significación real de la tabla de distribución t al buscar el valor t. Esto se debe a que cada cola de la distribución t toma la mitad del nivel de significación de cada uno.
Así que esta es una explicación de la tabla de distribución t en las estadísticas.
Recursos Relacionados
