Kalkulator Deviasi Standar

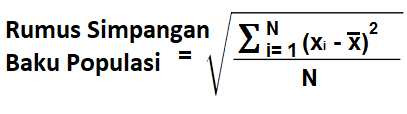
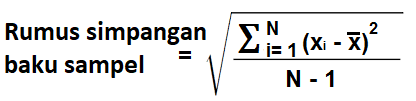
Simpangan Baku Populasi
Kalkulator Deviasi Standar Populasi menghitung simpangan baku suatu populasi.
Populasi mewakili seluruh kumpulan data. Ini termasuk setiap orang, barang, dll. Misalnya, jika kita berbicara tentang kelas yang terdiri dari 30 siswa, populasinya adalah 30 siswa. Ini berbeda dengan sampel (dibahas nanti), yang mewakili sebagian dari populasi. Misalnya, satu sampel dapat mengambil 10 siswa dan kemudian memeriksa data dan menarik kesimpulan dari 10 siswa tersebut untuk membuat kesimpulan tentang seluruh kelas.
Deviasi standar adalah ukuran statistik yang menunjukkan seberapa banyak variasi atau sebaran yang ada dalam kumpulan data dari meannya.
Standar deviasi yang rendah berarti tidak banyak variasi antara nilai data individu dari mean himpunan. Dengan kata lain, titik data cenderung sangat dekat dengan mean. Contoh kumpulan data dengan standar deviasi rendah adalah 2.21, 2.22, 2.23, 2.24, 2.25. Untuk kumpulan data ini, meannya adalah 2,23. Semua nilai data sangat dekat dengan nilai ini.
Deviasi standar yang tinggi berarti ada titik data yang cenderung memiliki rentang nilai yang luas; Dengan kata lain, titik data individu cenderung jauh dari mean. Oleh karena itu, nilainya sangat terpencar. Misalnya, data 0, 100 memiliki rata-rata 50. Namun, setiap titik data sangat jauh dari rata-rata 50. Kumpulan data ini memiliki standar deviasi yang sangat tinggi sehingga nilainya sangat jauh dari rata-rata.
Deviasi standar adalah ukuran yang penting dan banyak digunakan karena menunjukkan bagaimana data tersebar dari meannya. Ketika kita menghitung deviasi standar, kita tahu seberapa jauh skor cenderung berada dalam mean. Oleh karena itu, kita bisa mendapatkan perkiraan kasar tentang seberapa dekat nilai-nilai tersebut dalam satu standar deviasi. Misalnya, rata-rata tes adalah 80 dan standar deviasi 5. Ini berarti bahwa sebagian besar skor antara 75 dan 85, karena sebagian besar nilai dalam kumpulan data berada dalam deviasi standar rata-rata. Dan jika kita melakukan dua standar deviasi, hampir semua siswa akan mendapat nilai di antara nilai ini. Menurut Aturan Chebyshev, yang merangkum deviasi standar, setidaknya 75% dari seluruh populasi akan dinilai dalam 2 deviasi standar dari mean. Setidaknya 89% dari populasi akan mendapat skor dalam 3 standar deviasi rata-rata. Dan setidaknya 93,75% dari populasi akan mendapat skor dalam 4 standar deviasi rata-rata. Jadi, deviasi standar, secara statistik, memberi tahu kita banyak hal.
Untuk menggunakan kalkulator ini, pengguna hanya memasukkan kumpulan angka yang ingin mereka hitung deviasi standarnya, dengan setiap angka dipisahkan oleh titik koma. Titik koma harus digunakan untuk memisahkan nilai, atau kalkulator tidak akan berfungsi. Pembatas lain, termasuk spasi di antara angka, akan menyebabkan kalkulator tidak berfungsi. Hanya titik koma yang dikenali untuk memisahkan nilai. Setelah serangkaian angka dimasukkan, pengguna mengklik tombol "Menghitung" dan nilai deviasi standar yang dihasilkan dihitung dan ditampilkan.
Satuan yang dipecahkan oleh kalkulator deviasi standar sama dengan satuan yang Anda masukkan di bidang entri. Misalnya, jika nilai yang dimasukkan di kolom input dalam satuan inci, nilai deviasi standar yang dihasilkan akan dalam satuan inci. Unit tidak berubah dari input menjadi nilai yang dihasilkan.
Menghitung deviasi standar penting untuk berbagai tujuan statistik dan menyediakan cara lain untuk mengukur hasil kami.
Untuk elektronik, kita dapat memiliki nilai rata-rata arus, tegangan, dll. Dengan deviasi standar yang dihitung,
kita dapat menentukan berapa banyak deviasi standar yang diberikan arus, tegangan, dll. Di atas normalnya.
Ini dapat berguna untuk beberapa kemungkinan tujuan statistik.
Simpangan Baku Sampel
Kalkulator Deviasi Standar Sampel menghitung simpangan baku untuk sampel dari suatu populasi.
Sampel populasi mewakili sebagian populasi yang dipilih untuk tujuan statistik daripada seluruh populasi, seperti kalkulator di atas.
Simpangan baku suatu populasi dihitung secara berbeda dari keseluruhan populasi. Alih-alih membaginya dengan bilangan bulat dalam sampel, yang biasanya kita wakili sebagai N untuk mewakili jumlah penuh unit, kita membaginya dengan N-1. Ini akan selalu memastikan bahwa deviasi standar untuk sampel akan selalu lebih besar daripada deviasi standar untuk populasi.
Membagi dengan N-1 mungkin tampak seperti konvensi yang aneh, tetapi karena sampel tidak mewakili seluruh populasi, ahli matematika membagi dengan N-1 untuk menjelaskan fakta bahwa seluruh populasi tidak digunakan dan dengan demikian sampel akan sedikit lebih tinggi (nilainya naik sedikit).
Untuk menggunakan kalkulator ini, seperti yang terakhir, cukup masukkan daftar angka yang ingin Anda cari deviasi standarnya,
lalu klik tombol 'Hitung'. Simpangan baku dari angka tersebut akan dihitung dan ditampilkan secara otomatis.
Contoh penghitungan
Hitung simpangan baku dari angka-angka tersebut 3, 5, 7, 9, 11 y 17.
Jawabannya:
Simpangan Baku Populasi: 4,5338235029118
Simpangan Baku Sampel: 4,9665548085838: 7
Hitung simpangan baku dari angka-angka tersebut 1, 2, 3,5, 6,8, 9,7.
Jawabannya: Sumber Daya Terkait
Kalkulator Notasi Ilmiah
Simpangan Baku Populasi: 2,2983085567918
Simpangan Baku Sampel: 2,8148416178061
Kalkulator Angka Penting
Kalkulator Pembulatan Angka Penting
Kalkulator Pengujian Hipotesis
