Capacitor Discharge Calculator


Note: The resistance or capacitance value cannot be zero
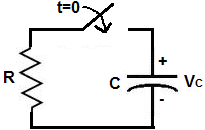
The Capacitor Discharge Calculator calculates the voltage that a capacitor with a a capacitance, of C, and a resistor, R, in series with it, will discharge to after time, t, has elapsed. You can use this calculator to calculate the voltage that the capacitor will have discharged after a time period, of t, has elapsed.
In order to calculate the voltage across the capacitor, we must know the initial voltage, V0, across the capacitor before the discharging begins, the capacitance, C, of the capacitor, the resistor, R, in series with the capacitor, and the amount of time that has elasped since the discharging began. Once we know these, we can calculate the voltage across the capacitor using the formula shown above.
The 3 variables which affect how the inital voltage discharges is time, t, the resistance of the resistor, R, and the capacitance of the capacitor, C.
The greater the amount of time has elapsed, the more the capacitor will discharge. The less time that has elapsed, the less time the capacitor has to discharge. Thus, the larger the t value, the smaller VC. The
The greater the resistance, R, of the resistor, the slower the discharge process will be. This is because resistance slows down the amount of current that passes through. Thus, if the resistance is large, the capacitor discharges more slowly. Therefore, the larger the resistance value, the greater VC is. The smaller the resistance, the smaller VC will be.
The greater the capacitance of the capacitor, the slower the discharge process will be. This is because the greater the capacitance, the more charge the capacitor has. If it has more charge, then it will take longer to discharge all of that charge. If the capacitance is smaller, it holds less charge. Therefore, it takes a shorter time to discharge that charge. Therefore, the higher the capacitance value, the greater VC will be. The smaller the capacitance, the smaller VC will be.
The value of the equation result gives VC, which is the voltage that is across the capacitor. The resultant voltage is in unit volts (V).
This calculator computes 2 values. It computes the amount of voltage the capacitor has discharged, which is what the capacitor discharge formula, above, calculates and it computes the amount of voltage remaining in the capacitor, which is equal to the initial voltage the capacitor has minus the amount of volts it has discharged.
Capacitor discharge is important for circuits which need capacitors to discharge voltage for operation. An example of such a circuit is a flash
camera. A flash camera is a camera which winds up to charge a capacitor and then when fully winded (charged up), dumps, or discharges, that charge so that a flash
can occur and a picture can be taken. Being able to calculate the voltage during any time in the discharge process for these type of circuits is crucial so that
the circuit can function properly, from a numerical value perspective.
Related Resources
Capacitor Code Calculator
Capacitance Calculator
Capacitor Charge Calculator
Capacitor Voltage Calculator
Capacitor Impedance Calculator
Capacitor Charging Calculator
Capacitor Energy Calculator
Capacitor Voltage Divider
Bypass Capacitor Calculator
Capacitor Equations
Capacitive Reactance
How to Calculate the Current Through a Capacitor
How to Calculate the Voltage Across a Capacitor
