Capacitor Equations

In this article, we show many capacitor equations.
Below is a table of capacitor equations.
This table includes formulas to calculate the voltage, current, capacitance, impedance, and time constant of a
capacitor circuit.
Capacitor Equations Table
| Equation | Description | Unit | Formula |
| Voltage | This equation calculates the voltage that falls across a capacitor. | Volts(V) | 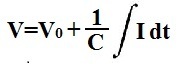 |
| Current | This equation calculates the current that goes through a capacitor. | Amperes(A) | 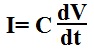 |
| Capacitance | This equation calculates the capacitance of a capacitor. | Farads(F) | 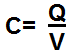 |
| Impedance | This equation calculates the impedance of a capacitor. | Ohms(Ω) | 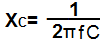 |
| Capacitor
Charge Voltage |
This equation calculates the amount of voltage that a capacitor will charge to at any given time, t, during the charging cycle. | Volts(V) | 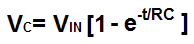 |
| Capacitor Discharge Voltage | This equation calculates the amount of voltage a capacitor will contain at any given time, t, during the discharge cycle. | Volts(V) |  |
| Capacitor Time Constant | This equation calculates the time constant of an RC circuit. | Seconds(S) | 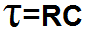 |
Now we'll go over the above equations below in more depth, so that you can get a greater undertstanding of these various capacitor formulas.
So in calculating the voltage across a capacitor, the voltage is equal to the amount of current that has charge (current) that has built up on one side of the capacitor. The more charge that falls across the plate of the capacitor that has built up charges makes for a greater voltage. Being that the capacitance of the capacitor affects the amount of charge the capacitor can hold, 1/capacitance is multiplied by the integral of the current. And, of course, if there is an initial voltage across the capacitor to begin with, we add this initial voltage to the voltage that has built up later to get the total voltage output.
In the next equation, we calculate the current across a capacitor. The current across a capacitor is equal to the capacitance of the capacitor multiplied by the derivative (or change) in the voltage across the capacitor. As the voltage across the capacitor increases, the current increases. As the voltage being built up across the capacitor decreases, the current decreases.
In the 3rd equation on the table, we calculate the capacitance of a capacitor, according to the simple formula, C= Q/V, where C is the capacitance of the capacitor, Q is the charge across the capacitor, and V is the voltage across the capacitor. It's a simple linear equation. Capacitance is defined by the unit charge a capacitor holds per unit volts.
In the next equation, we calculate the impedance of the capacitor. This is the resistance that a capacitor offers in a circuit depending on the frequency of the incoming signal. If the signal is a DC signal, meaning it has 0Hz frequency, plugging 0 into the formula, XC= 1/2πfC, we get an impedance of infinity. To DC voltage, a capacitor has a very high impedance, practically seen as infinite, so DC signals are unable to flow through capacitors. However, as we increase the frequency of the signal going through the capacitor, the capacitor offers less and less impedance (resistance). At a certain point, a high enough frequency, it's practically as if the capacitor is a short circuit, being that it offers practically no resistance. So this formula calculates impedance.
The next equation calculates the voltage that a capacitor charges up to when it is charging in a circuit. It charges exponentially, so you see the e function in the equation. The voltage it charges up to is based on the input voltage to the capacitor, VIN. The capacitor can charge up to a maximum value of the input voltage. It cannot exceed this input voltage. Thus, you see in the equationt that VC is VIN- VIN times the exponential function to the power of time and the RC constant. Basically, the more time that elapses the greater the value of the e function and, thus, the more voltage that builds across the capacitor.
The next equation calculates the voltage that a capacitor discharges to after a certain period of time has elapsed. The amount of voltage that a capacitor discharges to is based on the initial voltage across the capacitor, V0 and the same exponential function as present in the charging. A capacitor charges up exponentially and discharges exponentially. So the amount it discharges obviously includes how much voltage it has across it initially times the e function to the power of time and the RC constant. The more time that elapses, the more the capacitor discharges.
The last equation computes the time constant of an RC circuit, a circuit composed of a single resistor and capacitor.
The result of the product of the resistance times the capacitance is the time constant in unit seconds. If you take this result and find its inverse by
taking 1 and dividing it by this time value, you get the frequency. Both are very valuable for many circuits including
circuits where you need a particular time period or frequency.
So these are some of the most frequently seen capacitor equations. I can't say for a fact that it's all of them, it probably isn't, but it's definitely
a good amount and some of the most popular and widely used formulas for capacitors. These equations compute everything from the
voltage to the current, capacitance, charge, and time constant of capacitor circuits.
Related Resources
How to Calculate the Current Through a Capacitor
How to Calculate the Voltage Across a Capacitor
Capacitor Schematic Symbols
Inductor Equations
