Kirchhoff's Current Law (KCL)

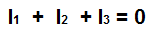
In this article, we explain Kirchhoff's current law (KCL).

KCL is a way of analyzing a circuit.

KCL states that the sum of all currents entering and leaving a node is equal to 0.

This is shown according to the formula, ΣI= 0.

KCL is essentially a principle of the conservation of charge.

What KCL really says, in simple terms, is that the sum of all currents entering a node is equal to the sum of all currents leaving the node.

KCL is a very powerful tool in circuit analysis that is used to find unknown voltage or current values in a circuit.

It is a type of nodal analysis, in which we can analyze each node of a circuit. Since KCL states that the sum of all currents entering a node must equal the sum of all currents leaving the node, we perform analysis on all nodes based on the inflow and outflow of current. We can use these nodal analsyis results to find unknown voltage and current values. We'll show how to do all these calculations below.

KCL Example

So, as an example, we'll use a very basic circuit with a single power supply and simply resistors, no other components.

The circuit we'll analyze with KCL is shown below.

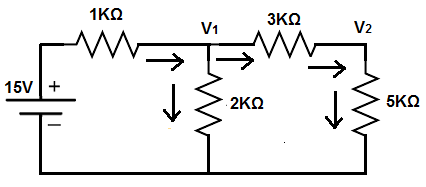
So we have a 15V power supply and we have 2 unknown voltages V1 and V2 that we want to calculate. Right now they're unknown but through a analysis with KCL, we can find the values of these voltages.

So how we do this is we do analyze on each of the 2 nodes of the circuits with KCL.

We get our numbers.

And then we can solve the linear system with linear algebra to solve for the unknown voltages, V1 and V2.

So let's start at the beginning.

So we already know the voltage of the first node; it's 15V. Therefore, we look at the other 2 nodes.

The first node with an unknown voltage is V1.

Using KCL, we look at all aspects of currents coming in and all aspects of current going out.

So judging from the power supply, current is coming into the node from the power supply and going out from the other 2 nodes. Usually, by convention, incoming current is negative and outgoing current is positive. You can have it the other way as well, but just be consistent, or else you'll get the wrong answer.

So the current that's coming in from the power supply is -(15-V1)/1KΩ. Or, if you rearrange it to get rid of the negative sign, it would be (V1 - 15)/1KΩ.

The next current (outgoing current) that goes down the 2KΩ resistor is V1/2KΩ.

The last current (outgoing current also) that goes through the 3KΩ resistor is (V1 - V2)/3KΩ.

So, in total, the equation for the first node is, after all reduction and simplifications is, 11V1 - 2V2 = 90.

We now look at the next node.

This node only has 2 currents, one ingoing current and one outgoing current.

The incoming current is the current that flows through the 3KΩ resistor. This gives us, (V1 - V2)/3KΩ. The outgoing current is the current that flows through the 5KΩ resistor. This gives us, V2/5KΩ.

So, in total, the equation for the second node, after all reduction and simplifications is, -5V1 + 8V2= 0.

So these produces the following equations shown below.

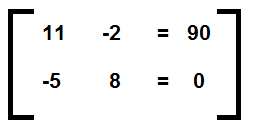
You can solve this, by hand, by rearranging equations, or you can use a systems of equations calculator. Plugging this into a 2x2 systems of equations calculator, this produces the answers, V1= 9.2V and V2 = 5.8V.

Using ohm's law, we calculate the currents going through each parts of the circuits.

The current going through the 1KΩ resistor is 5.8mA, since (15V-9.23V)/1KΩ= 5.77mA.

The current going through the 2KΩ resistor is 4.6mA, since 9.23V/2KΩ= 4.62mA.

The current going through the 3KΩ resistor is about 1.2mA, since (9.23V-5.77V)/3KΩ.

Doing KCL on the first node gives us, -5.8mA + 4.6mA + 1.2mA=0.

Therefore, there is a conservation of charge, which means our results are sound.

So KCL is a great tool for finding unknown values in circuits. It finds the unknown voltages, which then can be used to find unknown currents. It is also a great tool used to check to see if the results of a circuit are sound because it checks to see if there is a conservation of charge.

Related Resources

Kirchhoff's Voltage Law

Superposition Theorem

Thevenin's Theorem

Norton's Theorem

What is an Ideal Current Source?

What is a Constant Current Source?

RMS Voltage and Current- Explained