System of Equations Calculator

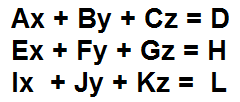
1x1 System of Equation Calculator

The 1x1 System of Equation Calculator calculates the solution to a linear equation containing one variable.

1x1 linear equations take on the form Ax=B where A is the coefficient of the variable and B is value that the equation is equal to.

To use this calculator, all a user must enter is the coefficient in front of the variable, which in this case is denoted by X, and the value that the equation is equal to.

Example

An example of a 1x1 linear equation is:

3x=6

Solution:
x=2

The coefficient in this case that is entered is 3 and the value that the equation is equal to is 6. If we take 6 and divide it by 3, we get our solution, which is x=2.

The 1x1 linear system of equation is the simplest of all linear equations.

---

2x2 System of Equations Calculator

The 2x2 System of Equation Calculator calculates the solution to 2 linear equations containing 2 variables.

2x2 linear equations take on the form:

Ax + By=C
Dx + Ey= F

where A, B, D, and E are the coefficients of the variable and C and F are the values that the equations are equal to.

To use this calculator, all a user must enter is the coefficients in front of the variables, which in this case are denoted by X and Y, and the values that the equations are equal to.

Example

An example of a 2x2 linear equation is:

x + 2y=3
4x + 5y=6

Solution:
x=-1, y=2

The coefficients that are entered in this case are 1, 2, 4, and 5 and the values that the equations are equal to are 3 and 6. If we take the first equation and solve for x, we get x= 3-2y. We then take this equation and plug it into the second equation and we get 4(3-2y) + 5y=6. Solving this, we get 12-8y+5y=6. This equals -3y=-6. Thus, y=2. Since we now know that y=2, we can plug this into any of the equations to solve for X. If we use the first equation, x + 2y=3, we get x + 2(2)=3. Thus, x=-1.

---

3x3 System of Equations Calculator

The 3x3 System of Equation Calculator calculates the solution to 3 linear equations containing 3 variables.

3x3 linear equations take on the form:

Ax + By + Cz=D
Ex + Fy + Gz=H
Ix + Jy + Kz=L

where A, B, C, E, F, G, I, J, and K are the coefficients of the variables and D, H, and L are the values that the equations are equal to.

To use this calculator, all a user must enter is the coefficients in front of the variables, which in this case are denoted by X, Y, and Z, and the values that the equations are equal to.

Example

An example of a 3x3 linear equation is:

x + 2y + 4z=4
2x + 5y + 12z=8
9x + 10y + 6z=20

Solution:
x=-28, y=32, z=-8

The coefficients that are entered in this case that is entered are 1, 2, 4, 2, 5, 12, 9, 10, and 6 and the values that the equations are equal to are 4, 8, and 20. Again, we can solve for X, Y, and Z by substition. If we take the first equation and solve for Z, we get Z= (4-x-2y)/4. We now take this Z value and plug it into the next equation. By doing this, we get 2x + 5y +12(4-x-2y/4). Solving for y, we get y= 4-x. We can then now plug this into the final equation. We plug in 4-x for y and (4-x-2(4-x))/4 for z. We do a double substition for the last so that we only have x variables in the last equation. Solving for X, we get x=-28. Since we know that x=-28 and wek now that y= 4-x, we know that y=32. Now plugging -28 for x and 32 for y in any of the equations yields -8 for z.

Substitution is one of the best and easiest methods for solving systems of equations.

System of equations is used in many different engineering and electronics applications. Two such uses are the mesh current analysis and kirchhoff's voltage loop analysis. When solving for mesh currents (KCL) and kirchhoff's voltage loop (KVL), systems of equations are the most common and widely used method to solve these current and voltage values.

Related Resources

Cross Product Calculator

FOIL Calculator- Multiplying Binomials

Exponential Calculator

How to Convert Degrees to Radians

How to Convert Radians to Degrees

Degrees to Radians Calculator

Radians to Degrees Calculator

Ratio Calculator