FOIL Calculator- Multiplying Binomials



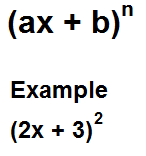
This binomial calculator calculates the product of a binomial raised either to the 2nd power or the 3rd power using the FOIL method. The product of the binomial expression is obtained, as with all products, by multiplying two binomial expressions together.

To use this calculator above, we follow the format (ax + b)ⁿ. A user just enters the a and b values. S/he can also change the sign and the exponent to which the binomial is raised. By default, the sign and exponent are "+" and "2". The user, however, can change the sign to "-" and the exponent to "3". Thus, the calculator allows for dynamic input.

Once the user clicks "Calculate", the answer will automatically be computed.

---

Multiplying Different Binomials

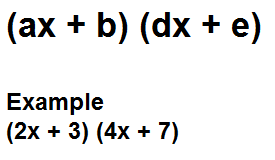
This binomial calculator calculates the product of two binomials which may be either the same or different. If they are the same, you could use the first calculator, but if they are different, then you must use this one.

Again, this calculates the product of the binomials by the FOIL method, the steps which are explained below.

---

FOIL Explained

Below is a reference visual of how FOIL works:

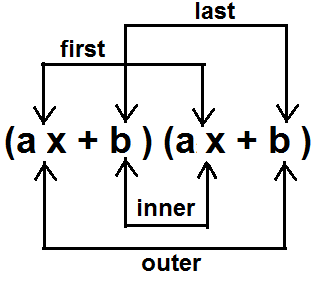
The FOIL is a method of binomial product calculation which utilizes the following steps shown below:

(ax + b)²

Let's say we have the following binomial which is shown above.

If we expand it without using the exponent, it will look like the following below:

(ax + b) (ax + b)

Using FOIL, we will calculate this binomial product by the following steps:

First- We take the first term from each binomial and multiply them together. With the binomial expression (ax + b)(ax +b), the first terms are ax and ax. This yields the product a²x².

Outer- Next, we take the outer or outside terms of the two binomials. With the binomial expression (ax + b)(ax +b), the outer terms are ax and b. This yields the product abx.

Inner- Next, we take the inner or insider terms of the two binomials. With the binomial expression (ax + b)(ax +b), the inner terms are b and ax. This yields the product abx. We now can combine the outer and inner terms, since they are like terms. Therefore, they simply add up to give the term 2abx.

Last- Next, we take the last terms of the two binomials. With the binomial expression (ax + b)(ax +b), the last terms are b and b. This yields the product b².

So now in total, once we add all the terms up, from this binomial expression, we get the end product of a²x² + 2abx + b².

Examples

(3x + 4)²

FOIL
First- (3x)(3x)=9x²
Outer- (3x)(4)= 12x
Inner- (4)(3x)= 12x
Last- (4)(4)=16

Total terms added together: 9x² + 12x + 12x +16 = 9x² + 24x + 16

(2x + 3)(5x - 7)

FOIL
First- (2x)(5x)=10x²
Outer- (2x)(-7)= -14x
Inner- (3)(5x)= 15x
Last- (3)(-7)= -21

Total terms added together: 10x² - 14x + 15x - 21 = 10x² + x - 21

Related Resources

Factoring Calculator

System of Equations Calculator

Exponential Calculator

Degrees to Radians Calculator

Radians to Degrees Calculator

Dot Product Calculator

Cross Product Calculator

Ratio Calculator

Significant Figures (Sig Fig) Calculator