Torque Calculator

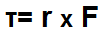
This torque calculator calculates the torque that is produced on an object based on the amount of force applied to the object at a distance, r, from the pivot point from where the force is applied to the object's pivot point.

Torque is a measure of the amount of force acting on object which causes the object to rotate.

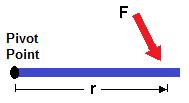
If you look in the above illustration, the vector, F, is the force vector, the circle leftmost is the pivot point, and the vector, r, represents the distance from where the force is applied on the object to the object's pivot point.

Distance and force are always vectors because they aren't just magnitudes. They have direction also. When force is applied to an object, it's applied at a certain angle and a certain direction. You can apply force straight down on an object. You can apply force at a 45° angle. This makes difference in the output torque value. Distance, also, is a vector, because it can be at an angle, which will affect the result of the calculation.

Torque is directly proportional to the magnitude of the force applied and the distance, r, from the pivot point. Thus, the greater the amount of force applied to an object, the greater the torque will be. Conversely, the less force applied, the less the torque will be. This is a pretty easy concept to understand. Imagine spinning a wheel. The harder you push, the greater the wheel rotates. The less force you push by, the less the spin of the wheel. In the same way as force, the distance is also directly proportional. The greater the distance from the pivot point the force is applied, the greater torque you can get. Conversely, the closer to the pivot point, the force is applied, the less torque you will get. Imagine pushing down a seesaw. If you push right at the middle, where the pivot point is located, you will have the hardest time getting it to move. If you push farther away (greater distance from the pivot point), it will be easier to move it.

To use this calculator, a user enters in the distance vector, r, and the force vector, F, and then clicks the 'Submit' button; the resultant value will be computed and automatically shown below. In standard convention, the distance vector is measured in unit meters (m). And the force vector is measured in unit newtons (N). The resultant value of the torque then would be N-m. However, you can put units you want. For example, if you use feet and newtons, the torque resultant will be in feet-newtons.

This calculator can be used for 2D vectors or 3D vectors. If a user is using this calculator for 2D vectors, which are vectors with only two dimensions, then s/he only fills in the i and j fields and leave the third field, k, blank. If using this calculator for a 3D vector, then the user enters in all fields.

The torque is calculated according to the formula, τ= rxF. This means that the cross product of the distance vector and the force vector gives the resultant. If you want more in-depth detail and the formula for how cross products are calculated, please visit the Cross Product Calculator of Vectors.

The resultant of a cross product is a vector value. So the resultant of torque is a vector value, and not simply just a scalar magnitude.

Torque is a very important calculation in engineering because anything that rotates needs torque to produce this rotation. This includes many electronic circuits that function by movement by rotation. A prime example of this would be an electric motor. An electric motor spins, or rotates, repeatedly. It needs a force, which is voltage, to produce this rotation applied at a certain distance from its pivot point. Calculating the amount of torque in circuits is very important.

---

Example Calculations
Calculate the torque produced from a vector with a distance of 7i + 3j + 9k meters and a force of 3i - 4j + 7k newtons.

Calculation:

r x F= [(3*7) - (9*-4)]i + [(9*3) - (7*7)]j + [(7*-4) - (3*3)]k= 57i -22j -37k

Calculate the torque produced from a vector with a distance of 2i + 5j - 6k meters and a force of 3i + 2j + 8k newtons.

Calculation:

r x F= [(5*8) - (-6*2)]i + [(-6*3) - (2*8)]j + [(2*2) - (5*3)]k= 52i -34j -11k

Related Resources

Dot Product Calculator

FOIL Calculator- Multiplying Binomials

Exponential Calculator

How to Convert Degrees to Radians

How to Convert Radians to Degrees

Degrees to Radians Calculator

Radians to Degrees Calculator

Ratio Calculator