Calculadora de Teste de Hipótese Estatística
Esta Calculadora de Teste de Hipótese Estatística determina se uma hipótese alternativa é verdadeira ou não. Aceitamos hipóteses verdadeiras e rejeitamos hipóteses falsas.
A hipótese nula é a hipótese que é reivindicada e que vamos testar contra.
A hipótese alternativa é a hipótese que acreditamos ser verdadeira.
Por exemplo, digamos que uma empresa afirma que só recebe 20 reclamações de consumidores em média um ano. No entanto, acreditamos que muito provavelmente ele recebe muito mais. Neste caso, a hipótese nula é a hipótese reivindicada pela empresa, que as queixas médias são 20 (μ = 20). A hipótese alternativa é que μ> 20, que é o que suspeitamos. Então, quando fazemos nossos testes, vemos qual hipótese é realmente verdadeira, o nulo (reivindicado) ou a alternativa (o que acreditamos que é).
O nível de significância que você seleciona determinará o quão ampla de uma área será a área de rejeição. O nível de significância representa a área de rejeição total de uma curva padrão normal. Portanto, se você optar por calcular com um nível de significância de 1%, você está escolhendo uma distribuição padrão normal que tem uma área de rejeição de 1% do total de 100%. Se você escolher um nível de significância de 5%, você está aumentando a área de rejeição para 5% dos 100%. Se você escolhe um nível de significância de 20%, aumenta a área de rejeição da curva normal padrão para 20% dos 100%. Quanto mais você aumentar o nível de significância, maior será a área de rejeição. Isso significa que há uma chance maior de uma hipótese será rejeitada e uma chance mais restrita de aceitar a hipótese, uma vez que a área de não rejeição diminui. Assim, quanto maior o nível de significância, menor ou mais estreita a área de não rejeição. Quanto menor o nível de significância, maior a área de não rejeição.
Existem 3 tipos de testes de hipótese que podemos fazer.
Há teste hipótese unilateral à esquerda, unilateral à direita,
Teste Hipótese Unilateral à Esquerda
Há teste hipótese unilateral à esquerda é ilustrado abaixo:

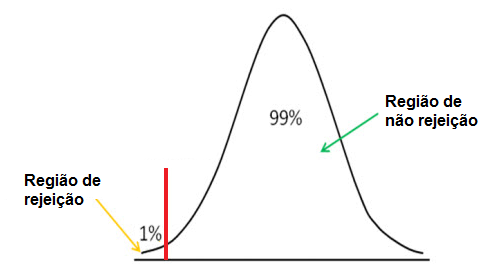
Usamos teste hipótese unilateral à esquerda para ver se a pontuação z está acima do ponto de corte de nível de significância, caso em que aceitamos a hipótese nula como verdadeira.
O método unilateral à esquerda, assim como a unilateral à direita, tem um ponto de corte. O nível de significância escolhido determina esse ponto de corte. Qualquer valor abaixo deste corte no método unilateral à esquerda representa a região de rejeição. Isto significa que se obtivermos uma pontuação z abaixo do ponto de corte, a pontuação z será na região de rejeição. Isso significa que a hipótese é falsa. Se a pontuação z está acima do ponto de corte, isso significa que ele está na região de não rejeição, e aceitamos a hipótese como verdadeira.
O método unilateral à esquerda é usado se quisermos determinar se uma média da
amostra é menor que a média da hipótese. Por exemplo, digamos que a média da hipótese é de
US $40.000, que representa o salário médio para os trabalhadores de saneamento, e
queremos determinar se esse salário tem diminuído nos últimos anos. Isso significa que
queremos ver se a média da amostra é menor do que a média da hipótese de US $40.000.
Este é um clássico teste de hipótese unilateral à esquerda, onde a média da amostra,
Teste Hipótese Unilateral à Direita
Teste Hipótese Unilateral à Direita é ilustrado abaixo:
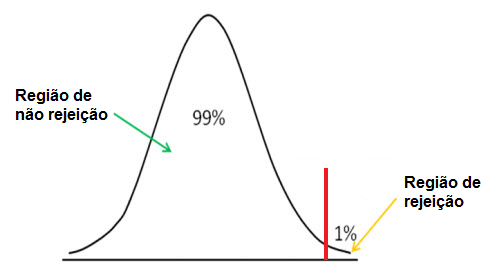
Usamos o teste de hipótese unilateral à direita para ver se a pontuação z está abaixo do ponto de corte de nível de significância, caso em que aceitamos a hipótese nula como verdadeira.
O método unilateral à direita, assim como o método unilateral à esquerda, tem um ponto de corte. O nível de significância escolhido determina esse ponto de corte. Qualquer valor acima deste corte no método da cauda direita representa a região de rejeição. Isto significa que se obtivermos uma pontuação z acima do ponto de corte, a pontuação z estará na área de rejeição. Isso significa que a hipótese de hipótese nula é falsa. Se o escore z estiver abaixo do ponto de corte, isso significa que ele está na região de não rejeição e aceitamos a hipótese como verdadeira.
O método unilateral à direita é usado se quisermos determinar se uma média da amostra é maior que a média da hipótese. Por exemplo, digamos que uma empresa alega que tem 400 acidentes de trabalho por ano. Isto significa que a hipótese nula é de 400. No entanto, suspeitamos que é tem muito mais acidentes do que isso. Portanto, queremos determinar se este número de acidentes é maior do que o que está sendo reivindicado. Isto significa que queremos ver se a média da amostra é maior do que a média da hipótese de 400. Este é um clássico teste hipótese unilateral à direita onde a média da amostra, H0. Esta é a hipótese alternativa. A hipótese nula é que a média é de 400 acidentes de trabalho por ano. E a Hipótese alternativa é que a média é superior a 400 acidentes por ano. Se a pontuação z calculada estiver acima do ponto de corte do nível de significância, isso significa que rejeitamos a hipótese nula e aceitamos a hipótese alternativa, porque a média da hipótese é muito menor do que a média real realmente é. Portanto, é falsa ea hipótese alternativa é verdadeira. Isso significa que realmente há mais de 400 acidentes de trabalho por ano ea alegação da empresa é imprecisa. Se a pontuação z está abaixo do ponto de corte do nível de significância, isso significa que aceitamos a hipótese nula e rejeitamos a hipótese alternativa que afirma que é mais, porque a média real é realmente menor que a média da hipótese. Isso realmente significa que há menos de 400 acidentes de trabalho por ano e reivindicação da empresa está correta.
Teste Hipótese Bilateral
Teste Hipótese Bilateral é ilustrado abaixo:
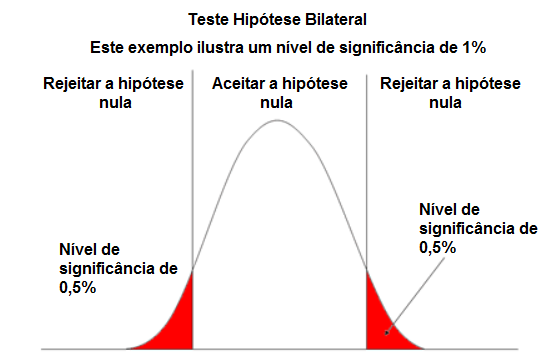
Usamos o método bilateral para ver se a média real da amostra não é igual ao que é reivindicado na média da hipótese.
Assim, se a média da hipótese é reivindicada como sendo 100. A hipótese alternativa pode alegar que a média da amostra não é 100.
O método bilateral tem 2 pontos de corte. O nível de significância que você escolhe determina esses pontos de corte. Se você escolher um nível de significância de 1%, os dois extremos da curva normal representarão cada um 0,5% para completar o nível de significância de 1%. Se você escolher um nível de significância de 5%, as 2 extremidades da curva normal serão cada um compreende 2,5% para fazer as extremidades.
Se a pontuação Z calculado estiver entre os 2 fins, aceitamos a
hipótese nula e rejeitamos a hipótese alternativa. Isso ocorre porque a pontuação
z será na região de não-rejeição. Se a pontuação z estiver fora deste intervalo,
então rejeitamos a hipótese nula e aceitamos a alternativa porque está fora do
intervalo. Portanto, a média da amostra é na verdade diferente da média da hipótese
nula, que é a média reivindicada.
Para usar esta calculadora, um usuário seleciona a média da hipótese nula (a média reivindicada), a média da amostra, o desvio padrão, o tamanho da amostra eo nível de significância e clica no botão 'Calcular'. A resposta resultante será automaticamente calculada e mostrada abaixo, com uma explicação quanto à resposta.
O teste de hipótese pode ser usado para qualquer tipo de
ciência para mostrar se rejeitamos ou aceitamos uma hipótese baseada na
computação quantitativa. Mesmo em certas áreas
da eletrônica, poderia ser útil.
Recursos Relacionados
Calculadora de Intervalo de Confiança
Calculadora de Notação Científica
Calculadora de Algarismos Significativos
Calculadora de Teste T de Student
