Kalkulator Faktorisasi

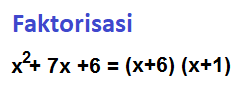
Kalkulator faktorisasi menghitung faktor-faktor yang membentuk a polinomial.
Kalkulator ini secara eksklusif menangani binomial dan trinomial. Ini tidak menghitung faktor dari jenis polinomial lainnya.
Binomial adalah polinomial yang mengandung 2 suku. Contoh binomial adalah x 2-36, 2x2-40, dan x2-100.
Trinomial adalah polinomial yang terdiri dari 3 suku. Contoh trinomial termasuk x2+3x+2, 2x2-14x-7, dan 7x2+5x-14.
Kalkulator ini menghitung faktor polinomial derajat ke-2, artinya nilai x pangkat tertinggi berasal dari derajat ke-2. Itu tidak melampaui level 2. Oleh karena itu, itu tidak menghitung kubus atau eksponen di atas 2.
Hal penting lain yang perlu diketahui tentang kalkulator ini adalah variabel harus x dalam pernyataannya. Ini adalah satu-satunya variabel yang dikenali kalkulator.
Ekspresi akan selalu difaktorkan jika ekspresi dapat difaktorkan, tetapi mungkin tidak selalu dikurangi sepenuhnya.
Kalkulator ini digunakan untuk elektronik karena elektronik membutuhkan matematika yang luas. Jadi persamaan pemfaktoran mungkin diperlukan dalam beberapa kasus.
Kalkulator faktorisasi ini menghitung faktor-faktor yang membentuk polinomial melalui sejumlah metode.
Salah satu metode umum yang dilakukan adalah kalkulator melihat semua suku dalam polinomial.
Lebih mudah untuk memvisualisasikan ini dengan contoh aktual, jadi kita akan melihat contoh sekarang.
x2 + 11x + 24
Jadi, dalam contoh ini, suku pertama adalah 1 dan suku terakhir adalah 24. Kalkulator akan mengalikan suku-suku ini untuk mendapatkan nilai 24. Nilai 24 ini sangat penting karena melambangkan suku terakhir polinomial. Jadi, setelah kita memperoleh nilai 24 ini, kalkulator kemudian melihat semua faktor dari 24, yaitu {1,24}, {2, 12}, {3,8}, dan {4,6}. Kalkulator kemudian melihat suku tengah. Ini melihat apakah ada faktor yang menambahkan hingga suku tengah. Jika ada faktor yang mendukung, maka itu cocok. Dan ini adalah faktor-faktor yang membentuk polinomial. Jadi dalam kasus ini, faktornya adalah 3 dan 8. Jadi jawaban akhirnya adalah (x+3)(x+8).
Ini adalah kasus jika semua nilainya positif.
Sekarang mari kita lihat contoh di mana tidak semua angka positif dan lihat bagaimana kalkulator ini memodifikasi.
Jadi, kita akan menggunakan nilai yang mirip dengan polinomial di atas, tetapi membuat suku terakhir negatif.
x2 -5x - 24
Jadi sekarang suku pertama adalah 1 dan suku terakhir adalah -24. Ini menghasilkan produk -24. Sekali lagi, kami menggunakan faktor dari 24 yaitu {1,24}, {2, 12}, {3,8}, dan {4,6}. Karena itu negatif, ini menyiratkan bahwa salah satu istilahnya negatif dan yang lainnya positif, karena satu-satunya cara untuk mendapatkan negatif adalah dengan positif dan negatif. Jadi ketika satu faktor negatif dan yang lainnya positif, angka-angka tersebut tidak menambah tetapi benar-benar mengurangi. Oleh karena itu, jika suku terakhir negatif, seperti dalam kasus ini, suku tengah adalah selisih faktor yang cocok. Karena suku tengahnya adalah -5 dalam kasus ini, faktor-faktornya adalah -8 dan 3. Jadi jawaban akhirnya adalah (x-8) (x + 3).
Ini adalah salah satu metode yang digunakan kalkulator untuk menghitung faktor polinomial.
Namun, metode ini tidak akan menangkap semua nilai.
Metode standar emas untuk menghitung faktor adalah melalui rumus kuadrat.
Dengan menggunakan rumus kuadrat di bawah ini, kita dapat menghitung faktor-faktor yang membentuk polinomial.
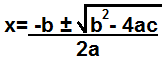
Rumus kuadrat menghitung 2 faktor yang membentuk polinomial.
Jika hasil rumus kuadrat muncul sebagai bilangan bulat, polinomial dapat difaktorkan. Jika hasilnya muncul sebagai pecahan, polinomial dapat difaktorkan tergantung pada nilai koefisien pertama. Jika hasilnya bukan bilangan bulat atau pecahan, polinomial tidak dapat difaktorkan.
Contoh polinomial dimana rumus kuadrat menghasilkan bilangan bulat ditampilkan di bawah ini.
x2 + 20x + 21
Memecahkan persamaan kuadrat menghasilkan faktor x = -1 dan x = -20. Kedua faktor ini adalah bilangan bulat.
Jadi, pemfaktoran akhir polinomial menghasilkan jawaban dari (x + 1) (x + 20).
Contoh polinomial di mana rumus kuadrat menghasilkan bilangan pecahan ditunjukkan di bawah ini.
18x2 +54x +28
Menyelesaikan persamaan kuadrat menghasilkan faktor x = -2 1/3 dan x = -2/3.
Tapi ini bukanlah jawaban akhir. Perhatikan bagaimana koefisien di depan suku pertama adalah 18. Jika kita membagi 18 menjadi faktor 6 dan 3, kita dapat mengalikan faktor-faktor ini dengan nilai yang diperoleh dalam rumus kuadrat untuk menghasilkan bilangan bulat. 6 * -2 1/3 =-14, jadi salah satu faktornya adalah -14. 3 * -2/3 = -2, jadi faktor lainnya adalah -2. Ini menghasilkan pemfaktoran polinomial untuk memberikan hasil akhir dari (6x + 14)(3x + 2).
Contoh polinomial yang menghasilkan hasil yang bukan keseluruhan maupun pecahan ditampilkan di bawah ini.
6x2 + 8x +4
Rumus kuadrat untuk persamaan ini tidak dapat diselesaikan. Jadi, persamaan ini tidak dapat difaktorkan.
Ini karena saat menyelesaikan rumus kuadrat di akar kuadrat, angkanya negatif.
Akar kuadrat untuk bilangan negatif tidak terdefinisi, sehingga persamaan tersebut tidak dapat diselesaikan.
Jadi, Anda dapat melihat betapa pentingnya rumus kuadrat dan bagaimana rumus itu digunakan untuk mencari faktor-faktor untuk sebuah polinomial (jika memfaktorkan dimungkinkan).
Oleh karena itu, kalkulator pemfaktoran ini sering menggunakan rumus kuadrat untuk melakukan penghitungan
guna melihat apakah polinomial dapat difaktorkan atau tidak.
Sumber Daya Terkait
Kalkulator Notasi Ilmiah
Kalkulator Deviasi Standar
Kalkulator Angka Penting
Kalkulator Pembulatan Angka Penting
Kalkulator Pengujian Hipotesis
