Magnitude Calculator

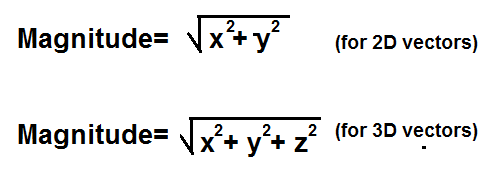
This Magnitude Calculator calculates the magnitude of a vector, based on the vector's 2-dimensional or 3-dimensional values.
This calculator can calculate the magnitude of both 2D and 3D vectors. To calculate the magnitude of a 2D vector, the user just enters in the vector's x and y values, and leaves the third field, the z value, blank. To calculate the magnitude of a 3D vector, a user enters in all 3 form fields, the vector's x, y, and z values.
No units have to be specified when solving for the magnitude. The resultant magnitude which is computed will be in the same unit as the unit of the input of the vector value. Thus, if you are calculating the magnitude of a force vector, and you enter the vector's components in newtons (N), the resultant magnitude will be in unit newtons as well.
Calculating the magnitude is a very significant calculation of a vector. The magnitude represents the total net scalar value of a vector. So, for example, if a force vector is 3i +4j + 0k N, it will have a net force of impact of 5 newtons of force.
Many engineering units are specified in vectors. Values such as force, magnetic field, velocity, etc. are specified with vector values. This is because these units not only
have magnitude, but they also have direction. Force is applied with a certain push or pull, but it isn't composed only of magnitude. It's also given in a certain direction. A force can be applied
straight vertically downward, applied at a 45° angle, at a 50° angle, and so forth. What angle it is applied at changes the net result in the action which occurs. When we solve for the magnitude
of a vector, we are solving simply for the net scalar value which that vector produces.
Example Calculations
Calculate the magnitude of the vector 5i - 7j +9k.
Calculation:
Resultant Magnitude: 12.45
Calculate the magnitude of the vector 3i - 14j - 21k.
Calculation:
Resultant Magnitude: 25.42
Related Resources
Dot Product Calculator
FOIL Calculator- Multiplying Binomials
Exponential Calculator
How to Convert Degrees to Radians
How to Convert Radians to Degrees
Degrees to Radians Calculator
Radians to Degrees Calculator
Ratio Calculator
Significant Figures (Sig Fig) Calculator
