Calculadora de Fatoração

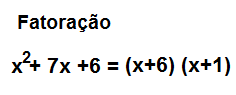
A calculadora de fatoração calcula os fatores que compreendem um polinômio.
Esta calculadora lida exclusivamente com binômios e trinômios. Ele não calcula os fatores de qualquer outro tipo de polinômio.
Um binômio é um polinômio que contém 2 termos. Exemplos de binômios são x2-36, 2x2-40, e x2-100.
Um trinômio é um polinômio que contém 3 termos. Exemplos de trinómios incluem x 2 + 3x + 2, 2x 2 -14x-7 e 7 2 + 5x-14.
Esta calculadora calcula o fatores de polinômios do 2 graus, significando que o
maior exponente x valor é do 2 graus. Não vai além do 2 graus.
Portanto, ele não calcula cubos ou expoentes acima de 2.
Outras coisas importantes a saber sobre esta calculadora é a variável deve ser x na expressão. Esta é a única variável que a calculadora reconhece. Mas essa funcionalidade está sendo trabalhada para receber qualquer variável.
A expressão será sempre fatorada se a expressão pode ser fatorada, mas nem sempre pode ser totalmente reduzida. Esta calculadora é uma calculadora de fatoração principalmente, não redutor. Mas essa funcionalidade será trabalhada.
Esta calculadora de fatoração calcula os factores que compreendem um polinómio através de um número de métodos.
Um método comum que é feito é que a calculadora olha para todos os termos no polinômio.
É mais fácil de visualizar com isso com um exemplo real, por isso vamos olhar para um exemplo agora.
x2 + 11x + 24
Assim, neste exemplo, o primeiro termo é 1 eo último termo é 24. A calculadora irá multiple estes termos em conjunto para obter o valor de 24. Este valor de 24 é muito importante porque representa o último termo de um polinómio. Então, uma vez que obtemos esse valor de 24, a calculadora então olha para todos os fatores de 24, que são {1,24}, {2, 12}, {3,8} e {4,6}. A calculadora então olha para o termo médio. Ele vê se algum dos fatores se somam ao médio prazo. Se qualquer um dos fatores, então é uma correspondência. E estes são os fatores que compõem o polinômio. Então, neste caso, os fatores são 3 e 8. Então a resposta final é (x + 3) (x + 8).
Este é o caso se todos os valores forem positivos.
Vamos agora olhar para um exemplo onde todos os números não são positivos e ver como esta calculadora modifica.
Então, usaremos valores semelhantes ao polinômio acima, mas tornar o último termo negativo.
x2 -5x - 24
Então, agora, o primeiro termo é 1 eo último termo é -24. Estes produzem um produto de -24. Novamente, usamos os fatores de 24 que são {1,24}, {2, 12}, {3,8}, e {4,6}. Sendo que é negativo isso implica que um dos termos é negativo e o outro é positivo, uma vez que a única maneira de obter um negativo é com um positivo e negativo. Então, quando um fator é negativo e o outro é positivo, os números não adicionam, mas realmente subtraem. Portanto, quando o último termo é negativo, como neste caso, o termo médio é a diferença dos fatores correspondentes. Sendo que o termo médio é -5, neste caso, os fatores são -8 e 3. Portanto, a resposta final é (x-8) (x + 3).
Este é um método que a calculadora usa para calcular os fatores de um polinômio.
No entanto, este método não captura todos os fatores.
Uma maneira poderosa de fatores de computação é através da computação de fórmula quadrática.
Usando a fórmula quadrática abaixo, podemos calcular os fatores que compõem um polinômio.
A fórmula quadrática calcula os 2 fatores que compõem um polinômio.
Se os resultados da fórmula quadrática surgirem como números inteiros, então o polinômio pode ser fatorado. Se os resultados surgem como números fracionários, então o polinômio pode ser capaz de ser fatorado dependendo do valor do coeficiente do primeiro. Se os resultados não podem nem números inteiros nem frações, então o polinômio não pode ser fatorado.
Um exemplo de um polinômio no qual a fórmula quadrática produz números inteiros é mostrado abaixo.
x2 + 20x + 21
Resolvendo a equação quadrática dá os fatores de x = -1 e x = -20. Ambos os fatores são números inteiros.
Assim, o fatoração final do polinômio dá a resposta de (x + 1) (x + 20).
Um exemplo de um polinômio no qual a fórmula quadrática produz números fracionários é mostrado abaixo.
18x2 +54x +28
Resolvendo a equação quadrática dá os fatores de x = -2 1/3 e x = -2 / 3.
Mas esta não é a resposta final. Observe como o coeficiente diante do primeiro termo é 18. Se dividimos 18 nos fatores 6 e 3, podemos multiplicar esses fatores pelos valores obtidos na fórmula quadrática para produzir números inteiros. 6 * -2 1/3 = -14, então um fator é -14. 3 * -2 / 3 = -2, então o outro fator é -2. Isto produz o fatoração do polinómio para dar o resultado final de (6x + 14) (3x + 2).
Um exemplo de um polinômio que produz resultados que não são nem inteiros nem fracionários é mostrado abaixo.
6x2 + 8x +4
A fórmula quadrática para esta equação não pode ser resolvida. Assim, esta equação não pode ser fatorada. Isso ocorre porque quando se resolve para a fórmula quadrática na raiz quadrada, o número é negativo. A raiz quadrada de um número negativo é indefinida, portanto, a equação não pode ser resolvida.
Assim, você pode ver como importante a fórmula quadrática pode ser e como é usado para encontrar fatores para um polinômio (se o fatoração é possível).
Portanto, esta calculadora de fatoração usa a fórmula quadrática fortemente para fazer cálculos para ver se o polinômio é factorável ou não.
Recursos Relacionados
Calculadora de Notação Científica
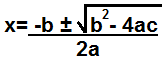
Calculadora de Algarismos Significativos
Calculadora de Intervalo de Confiança
Calculadora de Teste de Hipótese Estatística
Calculadora de Teste T de Student
