Kalkulator Sistem Persamaan Linear

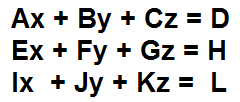
Sistem Persamaan Linear Satu Variabel

Sistem Persamaan Linear Satu Variabel menghitung solusi persamaan linier yang mengandung satu variabel.

Sistem Persamaan Linear Satu Variabel berbentuk Ax = B dengan A adalah koefisien variabel dan B adalah nilai persamaan.

Untuk menggunakan kalkulator ini, yang harus dimasukkan pengguna hanyalah koefisien di depan variabel, yang diwakili dalam hal ini X, dan nilai persamaan.

Contoh

Contoh sistem persamaan linear satu variabel adalah:

3x=6

Solution:
x=2

Koefisien dalam hal ini yang dimasukkan adalah 3 dan nilai persamaannya adalah 6 . Jika kita mengambil 6 dan membaginya dengan 3, kita mendapatkan solusi kita, yaitu x=2.

Sistem persamaan linear satu variabel adalah yang paling sederhana dari semua persamaan linier.

---

Sistem Persamaan Linear Dua Variabel

Sistem Persamaan Linear Dua Variabel menghitung solusi untuk 2 persamaan linier yang mengandung 2 variabel.

Sistem Persamaan Linear Dua Variabel memiliki bentuk:

Ax + By=C
Dx + Ey= F

di mana A, B, D, dan E adalah koefisien variabel dan C dan F adalah nilai persamaan.

Untuk menggunakan kalkulator ini, yang harus dimasukkan pengguna hanyalah koefisien di depan variabel, yang dalam hal ini dilambangkan dengan X dan Y, dan nilai persamaannya.

Contoh

Contoh persamaan sistem persamaan linear dua variabel adalah:

x + 2y=3
4x + 5y=6

Solusinya:
x=-1, y=2

Koefisien yang dimasukkan dalam kasus ini adalah 1, 2, 4, dan 5 dan nilai persamaannya adalah 3 dan 6. Jika kita mengambil persamaan pertama dan menyelesaikan x, kita mendapatkan x = 3-2y. Kami kemudian mengambil persamaan ini dan memasukkannya ke persamaan kedua dan kami mendapatkan 4 (3-2y) + 5y = 6. Memecahkan ini, kita mendapatkan 12-8y + 5y = 6. Ini sama dengan -3y = -6. Jadi, y = 2. Karena sekarang kita tahu bahwa y = 2, kita bisa memasukkannya ke salah satu persamaan untuk mencari X. Jika kita menggunakan persamaan pertama, x + 2y = 3, kita mendapatkan x + 2 (2) = 3. Jadi, x = -1.

---

Sistem Persamaan Linear Tiga Variabel

Sistem Persamaan Linear Tiga Variabel menghitung solusi untuk 3 persamaan linier yang mengandung 3 variabel.

Sistem Persamaan Linear Tiga Variabel memiliki bentuk:

Ax + By + Cz=D
Ex + Fy + Gz=H
Ix + Jy + Kz=L

di mana A, B, C, E, F, G, I, J, dan K adalah koefisien variabel dan D, H, dan L adalah nilai persamaan.

Untuk menggunakan kalkulator ini, pengguna harus memasukkan semua koefisien di depan variabel, yang dalam hal ini dilambangkan dengan X, Y, dan Z, dan nilai persamaannya.

Contoh

Contoh Sistem Persamaan Linear Tiga Variabel adalah:

x + 2y + 4z=4
2x + 5y + 12z=8
9x + 10y + 6z=20

Solution:
x=-28, y=32, z=-8

Koefisien yang dimasukkan dalam kasus ini adalah 1, 2, 4, 2, 5, 12, 9, 10, dan 6 dan nilai persamaannya adalah 4, 8, dan 20. Sekali lagi, kita dapat menyelesaikan X, Y, dan Z dengan substitusi. Jika kita mengambil persamaan pertama dan menyelesaikan Z, kita mendapatkan Z = (4-x-2y)/4. Sekarang kita ambil nilai Z ini dan masukkan ke persamaan berikutnya. Dengan melakukan ini, kita mendapatkan 2x + 5y +12 (4-x-2y/4). Memecahkan untuk y, kita mendapatkan y = 4-x. Sekarang kita bisa memasukkan ini ke dalam persamaan terakhir. Kami memasukkan 4-x untuk y dan (4-x-2(4-x))/4 untuk z. Kami melakukan substitusi ganda untuk yang terakhir sehingga kami hanya memiliki variabel x di persamaan terakhir. Memecahkan X, kita mendapatkan x = -28. Karena kita tahu bahwa x = -28 dan wek sekarang karena y = 4-x, kita tahu bahwa y = 32. Sekarang memasukkan -28 untuk x dan 32 untuk y di salah satu persamaan menghasilkan -8 untuk z.

Substitusi adalah salah satu metode terbaik dan termudah untuk menyelesaikan sistem persamaan.

Sistem persamaan digunakan dalam banyak aplikasi teknik dan elektronik yang berbeda. Dua kegunaan tersebut adalah analisis arus mesh dan analisis loop tegangan kirchhoff. Saat menyelesaikan arus mesh (KCL) dan loop tegangan kirchhoff (KVL), sistem persamaan adalah metode yang paling umum dan banyak digunakan untuk menyelesaikan nilai arus dan tegangan ini.

Sumber Daya Terkait

Kalkulator Notasi Ilmiah

Kalkulator Deviasi Standar

Kalkulator Angka Penting

Kalkulator Pembulatan Angka Penting

Kalkulator Faktorisasi

Kalkulator Pengujian Hipotesis