Hipotez Testleri Hesaplama
Bu Hipotez Testleri Hesaplama, alternatif bir hipotezin doğru olup olmadığını belirler. Doğru olup olmadığına bağlı olarak, hipotezi kabul edip etmemeyi belirler. Doğru hipotezleri kabul ediyor ve yanlış hipotezleri reddediyoruz.
Boş hipotez iddia edilen ve bizim doğrulayacağımız hipotezdir.
Alternatif hipotez, gerçekten olduğunu düşündüğümüz hipotezdir.
Örneğin, bir şirketin ortalama bir yılda yalnızca 20 tüketici şikayeti aldığını iddia ettiğini varsayalım. Ancak, büyük olasılıkla çok daha fazlasını alacağınıza inanıyoruz. Bu durumda, sıfır hipotezi, şirketin iddia ettiği ortalama şikayetin 20 (μ= 20) olduğu hipotezidir. Alternatif hipotez, şüphelendiğimiz şey olan μ > 20'dir. Yani testlerimizi yaptığımızda, hangi hipotezin gerçekten doğru olduğunu, boş (iddia edilen) veya alternatifi (ne olduğunu düşündüğümüz) görürüz.
Seçtiğiniz önem düzeyi, reddetme alanı olacak bir alanın genişliğini belirleyecektir. Anlamlılık seviyesi, normal bir standart eğrinin toplam reddetme alanını temsil eder. Bu nedenle, %1'lik bir anlamlılık düzeyinde hesaplamayı seçerseniz, toplam %100'ün% 1'i oranında bir ret alanına sahip standart bir normal dağılım seçmiş olursunuz. %5'lik bir önem düzeyi seçerseniz, reddedilme alanını %100'den %5'e yükseltmiş olursunuz. %20'lik bir anlamlılık düzeyinin seçilmesi, standart normal eğrinin reddetme alanını %100'ün %20'sine yükseltir. Önem düzeyini ne kadar artırırsanız, reddedilme alanı o kadar büyük olur. Bu, bir hipotezin reddedilme olasılığının daha yüksek olduğu ve reddetmeme alanı azaldığından hipotezi kabul etme olasılığının daha dar olduğu anlamına gelir. Bu nedenle, anlamlılık düzeyi ne kadar yüksek olursa, reddedilmeyen alan o kadar küçük veya daralır. Önem düzeyi ne kadar düşükse, reddedilmeme alanı o kadar büyüktür.
Yapabileceğimiz 3 tür hipotez testi vardır.
Sol kuyruklu hipotez testi, sağ kuyruklu hipotez testi ve çift taraflı hipotez testi vardır.
Sol Kuyruklu
Sol kuyruk hipotezinin testi aşağıda gösterilmektedir:

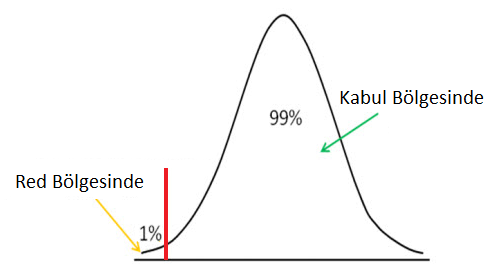
Z-puanının anlamlılık düzeyi kesme noktasının üzerinde olup olmadığını görmek için sol kuyruklu hipotez testlerini kullanırız, bu durumda boş hipotezin doğru olduğunu kabul ederiz.
Sol kuyruk yöntemi, sağ kuyruk gibi, bir kesme noktasına sahiptir. Seçtiğiniz önem seviyesi bu kesme noktasını belirler. Sol kuyruk yönteminde bu kesme noktasının altındaki herhangi bir değer, reddetme alanını temsil eder. Bu, kesme noktasının altında bir z-skoru alırsak, z puanının ret alanında olacağı anlamına gelir. Bu, hipotezin yanlış olduğu anlamına gelir. Z-puanı kesme noktasının üzerindeyse, bu, reddedilmeyen alanda olduğu anlamına gelir ve hipotezi doğru kabul ederiz.
Bir örnek ortalamasının hipotez ortalamasından düşük olup olmadığını belirlemek istiyorsak, sol kuyruk yöntemi kullanılır. Örneğin, hipotezin ortalamasının sanitasyon çalışanlarının ortalama maaşını temsil eden 40.000$ olduğunu varsayalım ve bu maaşın son yıllarda düşüp düşmediğini belirlemek istiyoruz. Bu, örnek ortalamanın 40.000$ 'lık hipotez ortalamasından düşük olup olmadığını görmek istediğimiz anlamına gelir. Bu, sol kuyruk hipotezinin klasik bir testidir. Z-puanı, anlamlılık düzeyi kesme noktasının altındaysa, bu, hipotezi reddettiğimiz anlamına gelir, çünkü hipotez, gerçek olandan çok daha yüksektir. Bu nedenle yanlıştır ve hipotezi reddediyoruz. Bu durumda, alternatif hipotez doğrudur. Z-puanı, anlamlılık düzeyi için kesme noktasının üstündeyse, bu, boş hipotezi kabul ettiğimiz ve bunun daha düşük olduğunu iddia eden alternatif hipotezi reddettiğimiz anlamına gelir, çünkü gerçek ortalama aslında hipotezin ortalamasından daha yüksektir.
Sağ Kuyruklu
Sağ kuyruk hipotezinin testi aşağıda gösterilmiştir:
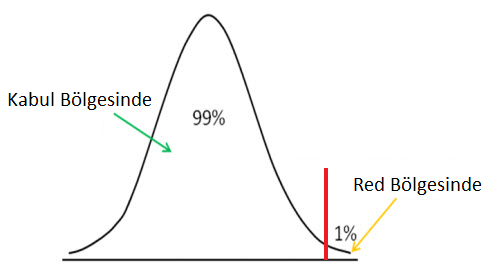
Z puanının anlamlılık düzeyi kesme noktasının altında olup olmadığını görmek için sağ kuyruklu hipotez testleri kullanırız, bu durumda sıfır hipotezinin doğru olduğunu kabul ederiz.
Sağ kuyruk yöntemi, sol kuyruk gibi, bir kesme noktasına sahiptir. Seçtiğiniz önem seviyesi bu kesme noktasını belirler. Sağ kuyruk yönteminde bu kesimin üzerindeki herhangi bir değer, reddetme alanını temsil eder. Bu, kesme noktasının üzerinde bir z-puanı elde edersek, z-puanının reddetme alanında olacağı anlamına gelir. Bu, boş hipotez ifadesinin yanlış olduğu anlamına gelir. Z-puanı kesme noktasının altındaysa bu, reddedilmeyen alanda olduğu anlamına gelir ve hipotezi doğru olarak kabul ederiz.
Bir örnek ortalamanın hipotez ortalamasından daha büyük olup olmadığını belirlemek istiyorsak, sağ kuyruk yöntemi kullanılır. Örneğin, bir şirketin yılda 400 işyeri kazası geçirdiğini iddia ettiğini varsayalım. Bu, boş hipotezin 400 olduğu anlamına gelir. Ancak, bundan çok daha fazla kaza geçirdiğinizden şüpheleniyoruz. Bu nedenle, bu kaza sayısının iddia edilenden fazla olup olmadığını belirlemek istiyoruz. Bu, örnek ortalamanın hipotez ortalaması olan 400'den büyük olup olmadığını görmek istediğimiz anlamına gelir. Bu, sağ kuyruk hipotezinin klasik bir testidir. Boş hipotez, ortalamanın yılda 400 iş kazası olduğudur. Ve alternatif hipotez, ortalamanın yılda 400 kazanın üzerinde olduğudur. Hesaplanan z-skoru, anlamlılık seviyesinin kesme noktasının üstündeyse, bu, boş hipotezi reddettiğimiz ve alternatif hipotezi kabul ettiğimiz anlamına gelir, çünkü hipotezin ortalaması, gerçek ortalamadan çok daha düşüktür. Bu nedenle yanlıştır ve alternatif hipotez doğrudur. Bu, aslında yılda 400'den fazla iş kazası olduğu ve şirketin iddiasının yanlış olduğu anlamına gelir. Z puanı, anlamlılık düzeyi için kesme noktasının altındaysa, bu, boş hipotezi kabul ettiğimiz ve daha fazla olduğunu iddia eden alternatif hipotezi reddettiğimiz anlamına gelir, çünkü gerçek ortalama, hipotez ortalamasından daha azdır. Bu, yılda 400'den az işyeri kazası olduğu ve şirketin iddiasının doğru olduğu anlamına gelir.
Çift Taraflı
Aşağıda iki kuyruklu bir hipotez testi bulunmaktadır:
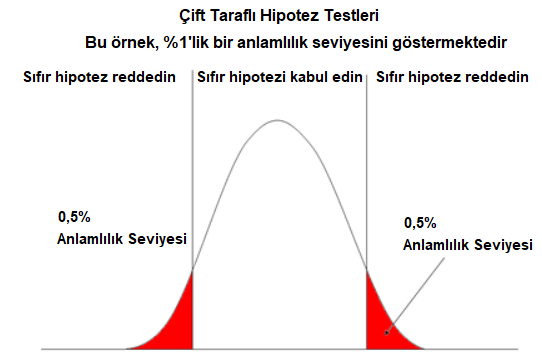
Gerçek örnek ortalamasının hipotez ortalamasında iddia edilene eşit olup olmadığını görmek için iki kuyruklu yöntemi kullanırız.
Bu nedenle, hipotezin ortalamasının 100 olması amaçlanıyorsa. Alternatif hipotez, örneğin ortalamasının 100 olmadığını söyleyebilir.
İki kuyruklu yöntemin 2 kesme noktası vardır. Seçtiğiniz önem seviyesi bu kesme noktalarını belirler. %1'lik bir anlamlılık düzeyi seçerseniz, normal eğrinin iki ucu %1'lik anlamlılık düzeyini temsil etmek için %0,5'i temsil edecektir. %5'lik bir anlamlılık düzeyi seçerseniz, normal eğrinin 2 ucunun her biri, uçları telafi etmek için %2,5'i oluşturacaktır.
Hesaplanan z-puanı 2 uç nokta arasındaysa, sıfır hipotezini kabul eder ve alternatif hipotezi
reddederiz. Bunun nedeni, z puanının reddedilmeme alanında olmasıdır. Z-puanı bu aralığın dışındaysa,
boş hipotezi reddeder ve aralığın dışında olduğu için alternatifi kabul ederiz.
Bu nedenle, örneklem ortalaması, iddia edilen ortalama olan boş hipotez ortalamasından aslında farklıdır.
Bu hesap makinesini kullanmak için, bir kullanıcı sıfır hipotezinin ortalamasını (iddia edilen ortalama), örnek ortalamayı, standart sapmayı, örneklem boyutunu ve önem düzeyini seçer ve 'Hesapla' düğmesini tıklar. Ortaya çıkan cevap otomatik olarak hesaplanacak ve cevabın açıklamasıyla birlikte aşağıda görüntülenecektir.
Hipotez testi, nicel hesaplamaya dayalı bir hipotezi reddettiğimizi veya kabul ettiğimizi
göstermek için herhangi bir bilim türü için kullanılabilir.
Bazı elektronik alanlarda bile faydalı olabilir.
alakalı kaynaklar
Bilimsel Gösterim Hesaplama
Güven Aralığı Hesaplama
çarpanlara ayırma hesap makinesi
Test Istatistiği Hesaplama
