Calculadora de Desviación Estándar

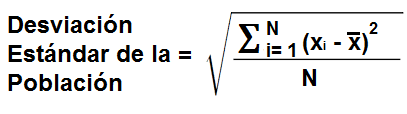
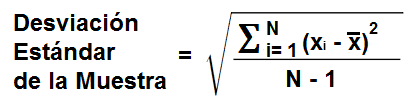
Desviación Estándar de la Población
La calculadora de desviación estándar de la población calcula la desviación estándar de una población.
Una población representa todo el conjunto de datos. Esto incluye a cada persona, artículo, etc. Por ejemplo, si estamos hablando de una clase de 30 estudiantes, la población sería de 30 estudiantes. Esto contrasta con una muestra (que se discute más adelante), que representa una parte de la población. Por ejemplo, una muestra puede tomar 10 estudiantes y después examinar los datos y sacar una conclusión de 10 estudiantes para hacer una conclusión sobre la clase entera.
Una desviación estándar es una medida estadística que muestra cuánta variación o dispersión hay en un conjunto de datos de su media.
Una desviación estándar baja significa que no hay mucha variación entre los valores de datos individuales de la media del conjunto. En otras palabras, los puntos de datos tienden a estar muy cerca de la media. Un ejemplo de un conjunto de datos con baja desviación estándar es 2,21, 2,22, 2,23, 2,24, 2,25. Para este conjunto de datos, la media es 2.23. Todos los valores de datos están muy cerca de este valor.
Una desviación estándar alta significa que hay puntos de datos que tienden a extenderse a lo largo de una amplia gama de valores; En otras palabras, los puntos de datos individuales tienden a estar lejos de la media. Por lo tanto, los valores están muy dispersos. Por ejemplo, los datos 0, 100 tienen una media de 50. Sin embargo, los puntos de datos individuales están muy lejos de la media de 50. Este conjunto de datos tiene una desviación estándar muy alta que los valores están tan separados de la media .
La desviación estándar es una medida importante y muy utilizada porque muestra cómo se extienden los datos de su media. Cuando calculamos la desviación estándar, sabemos hasta qué punto las puntuaciones tienden a situarse dentro de una media. Por lo tanto, podemos obtener una estimación aproximada de cómo los valores cercanos son de dentro de una desviación estándar. Por ejemplo, la media de una prueba es 80 y la desviación estándar es 5. Esto significa que la mayoría de las puntuaciones están entre 75 y 85, ya que la mayoría de los valores en un conjunto de datos están dentro de una desviación estándar de la media. Y si tuviéramos que salir a dos desviaciones estándar, casi todos los estudiantes habrían anotado entre este valor. De acuerdo con la Regla de Chebyshev, que resume las desviaciones estándar, por lo menos el 75% de toda la población se anotará dentro de 2 desviaciones estándar de la media. Al menos el 89% de la población obtendrá una puntuación dentro de las 3 desviaciones estándar de una media. Y por lo menos el 93.75% de una población anotará dentro de 4 desviaciones estándar de una media. Así, la desviación estándar, estadísticamente, nos dice mucho.
Para usar esta calculadora, un usuario sólo ingresa en el conjunto de números que desea calcular la desviación estándar de, con cada número separado por un punto y coma. Se debe utilizar un punto y coma para separar los valores, o bien la calculadora no funcionará. Cualquier otro delimitador, incluyendo un espacio entre números, hará que la calculadora no funcione. Sólo se reconocen puntos y comas para separar los valores. Una vez introducido el conjunto de números, el usuario hace clic en el botón "Calcular" y se calcula y visualiza el valor de la desviación estándar resultante.
Las unidades que la calculadora de desviación estándar resuelve son las mismas que las unidades que se introducen en el campo de entrada. Por ejemplo, si los valores introducidos en el campo de entrada están en pulgadas de unidad, el valor de desviación estándar resultante estará en unidades pulgadas. La unidad no cambia de entrada a valor resultante.
El cálculo de la desviación estándar es importante para muchos propósitos estadísticos diversos y proporciona otra manera de cuantificar nuestros resultados. Para la electrónica, podemos tener un valor promedio de corriente, voltaje, etc. Con la desviación estándar calculada, podemos determinar cuántas desviaciones estándar una corriente dada, voltaje, etc está por encima de su norma. Esto podría ser útil para varios propósitos estadísticos posibles.
Desviación Estándar de la Población
La Calculadora de Desviación Estándar de la Muestra calcula la desviación estándar para una muestra de una población.
Una muestra de una población representa una porción de la población elegida para fines estadísticos en lugar de toda la población, que es la calculadora anterior.
La desviación estándar de una población se calcula de forma diferente a toda una población. En lugar de dividir por el número entero de la muestra, que normalmente representamos como N para representar el número completo de unidades, dividimos por N-1. Esto siempre asegurará que la desviación estándar para una muestra siempre será algo mayor que la desviación estándar para la población.
La división por N-1 puede parecer una extraña convención, pero como una muestra no representa a toda la población, los matemáticos se dividen por N-1 para tener en cuenta el hecho de que no se usa la población completa y de esta manera la muestra será un poco más alto (que sube el valor un poco).
Para utilizar esta calculadora, al igual que la última, simplemente ingrese en la lista de números para la que desea encontrar la desviación estándar de, y luego haga clic en el botón 'Calcular'. La desviación estándar de los números será computada y mostrada automáticamente.
Ejemplos de Cálculos
Calcular la desviación estándar de los números 3, 5, 7, 9, 11 y 17.
Respuesta:
Desviación estándar de la Población: 4,5338235029118
Desviación estándar de la Muestra: 4,9665548085838: 7
Calcular la desviación estándar de 1, 2, 3,5, 6,8, 9,7.
Respuesta: Recursos Relacionados
Calculadora de Notación Científica
Desviación estándar de la Población: 2,2983085567918
Desviación estándar de la Muestra: 2,8148416178061
Calculadora de Factorización
Calculadora de Teorema de Chebyshev
Calculadora de Intervalo de Confianza
Calculadora de Prueba de Hipótesis Estadística
