Calculadora de Factorización

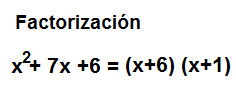
La calculadora de factorización calcula los factores que forman un polinomio.
Esta calculadora se ocupa exclusivamente de binomios y trinomios de segundo orden. No calcula los factores de ningún otro tipo de polinomio, como los de la tercera o cuarta orden.
Un binomio es un polinomio que contiene 2 términos. Ejemplos de binomios son x2-36, 2x2-40 y x2-100.
Un trinomio es un polinomio que contiene 3 términos. Ejemplos de trinomios incluyen x2+3x+2, 2x2-14x-7, y 72+5x-14.
Esta calculadora calcula el factor de polinomios del segundo grado, lo que significa que el exponente x de mayor valor es del segundo grado. No va más allá del segundo grado. Por lo tanto, no calcula cubos o exponentes por encima de 2.
Otras cosas importantes que debe saber sobre esta calculadora es que la variable debe ser x en la expresión. Esta es la única variable que la calculadora reconoce. Pero esta funcionalidad se está trabajando para tomar en cualquier variable.
La expresión siempre será factorizada si la expresión puede ser factorizada, pero no siempre se puede reducir completamente. Esta calculadora es una calculadora factoring principalmente, no reductor.
Esta calculadora de factorización calcula los factores que forman un polinomio a través de un número de métodos.
Un método común que se hace es que la calculadora mira todos los términos en el polinomio.
Es más fácil de visualizar con esto con un ejemplo real, por lo que vamos a ver un ejemplo ahora.
x2 + 11x + 24
Por lo tanto, en este ejemplo, el primer término es 1 y el último término es 24. La calculadora combinará estos términos para obtener el valor de 24. Este valor de 24 es muy importante porque representa el último término de un polinomio. Así que una vez que obtenemos este valor de 24, la calculadora examina todos los factores de 24, que son {1,24}, {2, 12}, {3,8} y {4,6}. La calculadora mira entonces el término medio. Ve si alguno de los factores se suma al medio plazo. Si alguno de los factores lo hace, entonces es un partido. Y estos son los factores que componen el polinomio. Entonces, en este caso, los factores son 3 y 8. Así que la respuesta final es (x + 3) (x + 8).
Este es el caso si todos los valores son positivos.
Veamos ahora un ejemplo en el que todos los números no son positivos y ver cómo esta calculadora modifica.
Por lo tanto, utilizaremos valores similares al polinomio anterior, pero haremos que el último término sea negativo.
x2 -5x - 24
Así que ahora el primer término es 1 y el último término es -24. Esto produce un producto de -24. De nuevo, usamos los factores de 24 que son {1,24}, {2, 12}, {3,8}, y {4,6}. Siendo que es negativo, esto implica que uno de los términos es negativo y el otro es positivo, ya que la única manera de obtener un negativo es con un positivo y un negativo. Así que cuando un factor es negativo y el otro es positivo, los números no añaden sino que realmente sustraen. Por lo tanto, cuando el último término es negativo, como en este caso, el término medio es la diferencia de los factores emparejados. Siendo que el término medio es -5 en este caso, los factores son -8 y 3. Así que la respuesta final es (x-8) (x + 3).
Este es un método que la calculadora utiliza para calcular los factores de un polinomio.
Sin embargo, este método no captura todos los valores utilizando este método.
El método estándar de oro de los factores de cálculo es a través del cálculo de la fórmula cuadrática.
Usando la fórmula cuadrática a continuación, podemos calcular los factores que forman un polinomio.
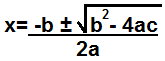
La fórmula cuadrática calcula los 2 factores que forman un polinomio.
Si los resultados de la fórmula cuadrática aparecen como números enteros, entonces el polinomio puede ser factorizado. Si los resultados aparecen como números fraccionarios, entonces el polinomio puede ser factorizado dependiendo del valor del coeficiente de la primera. Si los resultados no pueden ni números enteros ni fracciones, entonces el polinomio no puede ser factorizado.
Un ejemplo de un polinomio en el que la fórmula cuadrática produce números enteros se muestra a continuación.
x2 + 20x + 21
Resolviendo la ecuación cuadrática se obtienen los factores de x = -1 y x = -20. Ambos factores son números enteros.
Por lo tanto, el factoraje final del polinomio da la respuesta de (x + 1) (x + 20).
Un ejemplo de un polinomio en el que la fórmula cuadrática produce números fraccionarios se muestra a continuación.
18x2 +54x +28
Resolviendo la ecuación cuadrática se obtienen los factores de x= -2 1/3 y x = -2/3.
Pero esta no es la respuesta final. Observe cómo el coeficiente frente al primer término es 18. Si dividimos 18 en los factores 6 y 3, podemos multiplicar estos factores por los valores obtenidos en la fórmula cuadrática para producir números enteros. 6 * -2 1/3 = -14, por lo que un factor es -14. 3 * -2 / 3 = -2, por lo que el otro factor es -2. Esto produce el factoraje del polinomio para dar el resultado final de (6x + 14) (3x + 2).
A continuación se muestra un ejemplo de un polinomio que produce resultados que no son ni enteros ni fraccionarios.
6x2 + 8x +4
La fórmula cuadrática para esta ecuación no puede ser resuelta. Por lo tanto, esta ecuación no puede ser factorizada. Esto es porque al resolver para la fórmula cuadrática en la raíz cuadrada, el número es negativo. La raíz cuadrada de un número negativo no está definida, por lo que la ecuación no puede resolverse.
Así puede ver cuán importante puede ser la fórmula cuadrática y cómo se utiliza para encontrar factorajes para un polinomio (si es posible factorizar).
Por lo tanto, esta calculadora factoring utiliza la fórmula cuadrática fuertemente para hacer cálculos para ver si el polinomio es factorable o no.
Recursos Relacionados
Calculadora de Notación Científica
Calculadora de Teorema de Chebyshev
Calculadora de Intervalo de Confianza
Calculadora de Prueba de Hipótesis Estadística
Calculadora de Cifras Significativas
Calculadora del Redondeo de Cifras Significativas
Calculadora de Prueba T para Muestras Relacionadas
Calculadora de Prueba T para Muestras Independientes
Calculadora de Valor de p
