Calculadora de Prueba de Hipótesis Estadística
Esta Calculadora de Prueba de Hipótesis determina si una hipótesis alternativa es verdadera o no. Basado en si es verdad o no determina si aceptamos o rechazamos la hipótesis. Aceptamos hipótesis verdaderas y rechazamos hipótesis falsas.
La hipótesis nula es la hipótesis que se reivindica y que vamos a verificar.
La hipótesis alternativa es la hipótesis que creemos que realmente es.
Por ejemplo, digamos que una compañía afirma que sólo recibe 20 quejas de consumidores en promedio un año. Sin embargo, creemos que lo más probable es que recibe mucho más. En este caso, la hipótesis nula es la hipótesis reivindicada por la empresa, que las quejas promedio es de 20 (μ = 20). La hipótesis alternativa es que μ> 20, que es lo que sospechamos. Así que cuando hacemos nuestras pruebas, vemos qué hipótesis es realmente verdadera, la nula (reclamada) o la alternativa (lo que creemos que es).
El nivel de significación que seleccione determinará la amplitud de un área que será el área de rechazo. El nivel de significación representa el área de rechazo total de una curva estándar normal. Por lo tanto, si elige calcular con un nivel de significancia de 1%, está eligiendo una distribución estándar normal que tiene un área de rechazo del 1% del total 100%. Si elige un nivel de significación del 5%, está aumentando el área de rechazo al 5% del 100%. Si elige un nivel de significación del 20%, aumenta el área de rechazo de la curva normal estándar hasta el 20% del 100%. Cuanto más aumentas el nivel de significación, mayor es el área de rechazo que hay. Esto significa que hay una mayor probabilidad de que una hipótesis sea rechazada y una posibilidad más estrecha de aceptar la hipótesis, ya que el área de no rechazo disminuye. Por lo tanto, cuanto mayor es el nivel de significación, más pequeño o más estrecho es el área de no rechazo. Cuanto menor sea el nivel de significación, mayor será el área de no rechazo.
Hay 3 tipos de pruebas de hipótesis que podemos hacer.
Hay cola izquierda, cola derecha y dos pruebas de hipótesis de cola.
Cola Izquierda
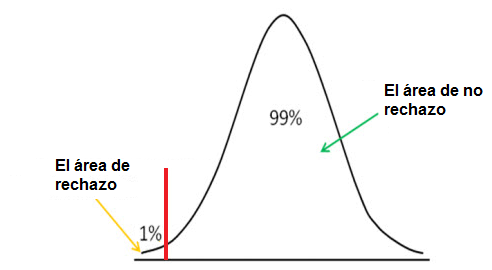
La prueba de la hipótesis de la cola izquierda se ilustra a continuación:

Utilizamos pruebas de hipótesis de cola izquierda para ver si la puntuación z está por encima del punto de corte de nivel de significación, en cuyo caso aceptamos la hipótesis nula como verdadera.
El método de la cola izquierda, al igual que la cola derecha, tiene un punto de corte. El nivel de significación que elija determina este punto de corte. Cualquier valor por debajo de este punto de corte en el método de cola izquierda representa el área de rechazo. Esto significa que si obtenemos una puntuación z por debajo del punto de corte, la puntuación z estará en el área de rechazo. Esto significa que la hipótesis es falsa. Si la puntuación z está por encima del punto de corte, esto significa que está en el área de no rechazo, y aceptamos la hipótesis como verdadera.
El método de la cola izquierda se utiliza si queremos determinar si una media de la muestra es menor que la media de la hipótesis.
Por ejemplo, digamos que la media de la hipótesis es de $40,000, lo que representa el salario promedio de los trabajadores de saneamiento,
y queremos determinar si este salario ha ido disminuyendo en los últimos años. Esto significa que queremos ver si la media de la muestra
es menor que la media de la hipótesis de $40.000. Esta es una prueba clásica de la hipótesis de la cola izquierda, donde la media de la
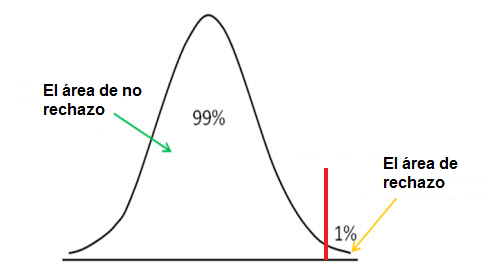
muestra, La prueba de la hipótesis de la cola derecha se ilustra a continuación: Utilizamos pruebas de hipótesis de cola derecha para ver si la puntuación z está por debajo del punto de corte de nivel de significación,
en cuyo caso aceptamos la hipótesis nula como verdadera.
El método de la cola derecha, al igual que la cola izquierda, tiene un punto de corte. El nivel de significación
que elija determina este punto de corte. Cualquier valor por encima de este corte en el método de la cola derecha representa el
área de rechazo. Esto significa que si obtenemos una puntuación z por encima del punto de corte, la puntuación z estará en el área de
rechazo. Esto significa que la afirmación de hipótesis nula es falsa. Si la puntuación z está por debajo del punto de corte,
esto significa que está en el área de no rechazo, y aceptamos la hipótesis como verdadera.
El método de la cola derecha se utiliza si queremos determinar si una media de la muestra es mayor que la media de la hipótesis. Por ejemplo, digamos que una empresa afirma que tiene 400 accidentes de trabajo al año. Esto significa que la hipótesis nula es 400. Sin embargo, sospechamos que tiene muchos más accidentes que esto. Por lo tanto, queremos determinar si este número de accidentes es mayor que lo que se reclama. Esto significa que queremos ver si la media de la muestra es mayor que la media de la hipótesis de 400.
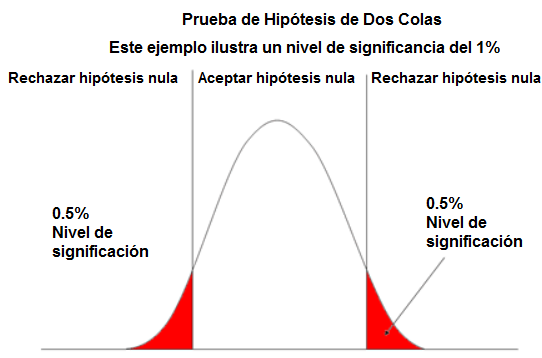
Se trata de una prueba clásica de la hipótesis de la cola derecha, donde la media de la muestra, A continuación se muestra una prueba de hipótesis de dos colas: Usamos el método de dos colas para ver si la media real de la muestra no es igual a lo que se reclama en la media de la hipótesis.
Por lo tanto, si se pretende que la media de la hipótesis sea 100. La hipótesis alternativa puede afirmar que la media de la muestra no es 100.
El método de dos colas tiene 2 puntos de corte. El nivel de significación que elija determina estos puntos de corte. Si elige un nivel de significación del 1%, los dos extremos de la curva normal representarán el 0,5% para representar el nivel de significación del 1%. Si elige un nivel de significación del 5%, los 2 extremos de la curva normal comprenderán cada uno un 2,5% para compensar los extremos.
Si la puntuación z calculada está entre los 2 extremos, aceptamos la hipótesis nula y rechazamos la hipótesis alternativa. Esto se debe a que la puntuación z estará en el área de no rechazo. Si la puntuación z está fuera de este rango, entonces rechazamos la hipótesis nula y aceptamos la alternativa porque está fuera del rango. Por lo tanto, la media de la muestra es realmente diferente de la media de la hipótesis nula, que es la media que se reclama.
Para usar esta calculadora, un usuario selecciona la media de la hipótesis nula (la media que se reclama), la media de la muestra, la desviación estándar, el tamaño de la muestra y el nivel de significación y hace clic en el botón 'Calcular'. La respuesta resultante se calculará automáticamente y se mostrará a continuación, con una explicación de la respuesta.
La prueba de hipótesis se puede utilizar para cualquier tipo de ciencia para demostrar si rechazamos o aceptamos una hipótesis basada en la computación cuantitativa. Incluso en ciertas áreas de la electrónica, podría ser útil.
Recursos Relacionados
Calculadora de Valor de p
Dos Colas
Calculadora de Prueba T de Student
Calculadora de Prueba T para Muestras Relacionadas
Calculadora de Prueba T para Muestras Independientes
Calculadora de Valor Esperado
Calculadora de Teorema de Chebyshev
Calculadora de Intervalo de Confianza
Calculadora de Cifras Significativas
Calculadora del Redondeo de Cifras Significativas
