Bernoulli Ungleichung Rechner

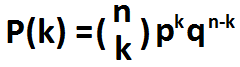
Dieser Bernoulli Ungleichung Rechner berechnet die Wahrscheinlichkeit eines Ereignisses.

Die Formel für die Berechnung der Ergebnisse der Bernoulli Ungleichung ist unten gezeigt:

Der Bernoulli-Versuch wird durch Multiplizieren des Binomialkoeffizienten mit der Wahrscheinlichkeit des Erfolgs mit der k-Leistung multipliziert mit der Wahrscheinlichkeit eines Versagens mit der n-k-Leistung berechnet.

repräsentiert den Binomialkoeffizienten. Der Binomialkoeffizient stellt die Gesamtzahl der verschiedenen Kombinationen dar, die k Elemente aus insgesamt n Auswahlen nehmen können. Wenn wir z. B. insgesamt 7 Elemente haben und 5 Elemente aus diesen 7 wählen wollen, so sind n = 7 und k-5, und der Binomialkoeffizient wäre gleich 21. Dies bedeutet, dass es 21 verschiedene mögliche Kombinationen gibt Kann 5 Einzelteile ordnen, wenn er von insgesamt 7 Einzelteilen genommen wird. organiser 5 articles quand pris sur un total de 7 articles.

p^k repräsentiert die Wahrscheinlichkeit des Auftretens des Ereignisses. Es steht für die Erfolgsrate, die das Ereignis eintritt.

q^n-k repräsentiert die Wahrscheinlichkeit, dass das Ereignis nicht auftritt. Sie repräsentiert die Ausfallrate des Ereignisses.

Wenn wir alle diese Variablen und multiplizieren sie zusammen, erhalten wir das Ergebnis der Bernoulli Ungleichung. Die bernoulli Studie stellt die Wahrscheinlichkeit des Erfolgs (die ein Ereignis auftreten wird).

Die Berechnung der Bernoulli Ungleichung kann nur unter den folgenden Umständen erfolgen.

1. 2 Ergebnisse nur- Wenn es nur 2 mögliche Ergebnisse, die meiste Zeit als Erfolg oder Misserfolg aus. Dies kann viele verschiedene Ergebnisse wie Köpfe oder Schwänze darstellen, gewinnen oder verlieren, gehen oder gehen nicht. Es kann nur getan werden, wenn es genau 2 Ergebnisse. Die meisten der Zeit wird es als Erfolg oder Misserfolg ausgedrückt werden.
2. Jeder Versuch muss unabhängig sein - Jeder Versuch (jedes Mal, wenn das Ereignis eintritt) muss unabhängig voneinander sein. Das bedeutet, dass die Ereignisse völlig unabhängig sind; Sie hängen nicht von der vorherigen Studie oder der Studie nach. Ein klassisches Beispiel sind Köpfe oder Schwänze. Jeder Flip ist unabhängig von allen anderen.
3. Erfolgswahrscheinlichkeit ist bei jedem Versuch gleich - Die Wahrscheinlichkeit, dass das Ereignis auftritt oder der Erfolg im gewünschten Ergebnis liegt, muss identisch sein. Zum Beispiel, für jeden Flip einer Münze, gibt es immer eine 50% Erfolgsrate der immer ein Köpfe. Mit anderen Worten, die Wahrscheinlichkeit eines Ereignisses muss für jeden Versuch gleich sein, nicht anders.

Wenn alle diese Bedingungen erfüllt sind, können wir Bernoulli Ungleichung anwenden, um das Prozentergebnis zu finden, das ein Ereignis eintritt.

Um bernoulli Studie zu veranschaulichen, gehen wir durch ein konkretes Beispiel, wo Bernoulli Ungleichung verwendet werden würde.

Nehmen wir an, es gibt eine Prüfung, wo 60% der Studierenden passieren. Dies ist die Freshmen Aufnahmeprüfung. Wenn 7 Neulinge die Prüfung nehmen, was wird dann die Wahrscheinlichkeit sein, dass 5 Pass. In diesem Beispiel ist n=7, k=5, und die Erfolgsquote beträgt 60% oder .6. Die Fehlerrate beträgt dann 1-.6 = 0,4 oder 40%. Mit diesen Zahlen, stecken wir sie in die Formel. Der Binomialkoeffizient von n=7 und k=5 ist 21. Wir haben dann P (k) = 21 (.6) ⁵ (4)² =. 2613 oder 26,13%. Diese 26,13% ist Erfolgsrate, dass 5 von 7 Neulingen die Prüfung bestehen wird.

Um diesen Rechner zu benutzen, gibt der Benutzer einfach nur die n- und k-Werte ein, nur mit der Wahrscheinlichkeit, dass das Ereignis eintritt. Sie oder er klickt dann auf die Schaltfläche "Berechnen", und die resultierende bernoulli Testberechnung wird automatisch berechnet und angezeigt.

Bernoulli Ungleichung kann für jede wissenschaftliche Berechnungen verwendet werden.

Ähnliche Ressourcen

Tschebyscheff-Ungleichung Rechner

Konfidenzintervall Rechner

Hypothesentest Rechner

Signifikante Stellen Rechner

Runden Signifikante Stellen Rechner

Wissenschaftliche Schreibweise Rechner

Faktorisierung Rechner