Signifikante Stellen Rechner

Dieser Signifikante Stellen rechner berechnet die Anzahl der signifikanten stellen einer Zahl und gibt an, welche stellen sind signifikant.
Signifikante Ziffern sind die Werte in einer Zahl, die gezählt werden kann, um genau zu sein. Signifikante Ziffern in einer Zahl sind diejenigen Werte, die mit Sicherheit oder einem hohen Maß an Vertrauen bekannt sein können, während unwesentliche Ziffern diejenigen sind, denen wir nicht so sehr genau vertrauen.
Signifikante Ziffern werden ausgiebig für Messungen verwendet. Verschiedene Messwerkzeuge können Messungen mit unterschiedlicher Genauigkeit aufzeichnen. Einige Messwerkzeuge zeichnen viel detaillierter auf als andere Messwerkzeuge. Wenn wir zum Beispiel ein Lineal haben, das nur Zentimeter misst, können wir bis zu einem Hundertstel Meter messen. Wenn wir nun das Lineal wechseln und ein Millimeter messen, können wir bis zu einem Tausendstel Meter rechnen. So können wir eine zusätzliche signifikante Zahl haben, da das Lineal detaillierter ist und eine höhere Genauigkeit der Messung ermöglicht.
Es ist wichtig, um ehrlich zu sein, wenn Sie eine Messung, so dass der resulante Wert nicht scheinen, um genauer als die Ausrüstung verwendet, um die Messung ermöglicht. Und wie wir den aufgezeichneten Wert ehrlich zu machen, ist durch die Kontrolle der Anzahl der Ziffern, oder signifikante Zahlen, verwendet, um die Messung Bericht. Der aufgezeichnete Wert darf keine signifikanten Stellen enthalten, die das Messwerkzeug zulässt.
So, zum Beispiel, wenn wir eine Messung nehmen und wir können den Wert ist 230 Gramm. Die 2 und 3 sind signifikante Stellen, während die 0 nicht. Die 0 ist unsicher, weil wir nicht vertrauen, dass es richtig ist. Für die Zahl 230 sind nur die 2 und 3 mit hoher Genauigkeit bekannt, während die 0 sozusagen unsicher und nicht vertrauenswürdig ist. Somit hat die Zahl 230 nur 2 signifikante Stellen.
Beispielsweise misst eine Portoskala in Gramm. Es kann nicht ein Zehntel eines Gramm, ein Hundertstel eines Gramms, etc., nur in Gramm messen. Es dauert eine Messung in Gramm +/- 1 Gramm. Daher kann es nur auf die Genauigkeit von 1 signifikanten Ziffer zu messen. Eine Zweiwannen-Waage kann jedoch bis zu einem Hundertstel eines Gramm messen. Daher wird es 3 signifikante Stellen haben, eine für den Platz, eine für den zehnten Platz und eine für den Hundertstel. Eine analytische Balance kann bis zu einem Tausendstel eines Gramms messen, so dass es bis zu 4 signifikante Stellen haben kann.
Bei all diesen Messgeräten, die oben diskutiert wurden, müssen jedoch die korrekten signifikanten Stellen eingehalten werden. Stellen Sie sich vor, wenn ein Messgerät nur bis ein Hundertstel eines Gramm wie das Zwei-Pfanne-Gleichgewicht messen kann und wir sagen, dass es eine Messung auf ein Tausendstel eines Gramms aufzeichnet. Dies würde unsere Ergebnisse sehr verdächtig machen und es wäre ungenau. Wenn ein Gerät nur bis ein Hundertstel eines Gramms messen kann, wie kann man einen Wert erhalten, der genauso genau ist wie ein Tausendstel Gramm. Daher können signifikante Zahlen in der wissenschaftlichen Gemeinschaft sehr wichtig sein. Es zeigt, wie genau eine Zahl ist, basierend auf der Anzahl der signifikanten Stellen in der Zahl.
Nun, da Sie wissen, die Bedeutung der signifikanten Zahlen, gehen wir über die Regeln für die Entscheidung, welche Ziffern in einer Zahl sind signifikant und die unbedeutend sind.
Regeln
∙ Alle Zahlen, die nicht Null sind, sind signifikant.
Ex. 5,4789- Alle Ziffern sind ungleich null. Daher sind alle Ziffern signifikant. So hat es 5 signifikante Stellen.
∙ Nullen, die sich zwischen Ziffern ungleich Null befinden, sind signifikant.
Ex. 2,00008- Alle Nullen in dieser Reihe sind signifikant. Der Daher hat es 6 signifikante Stellen.
∙ Nullen am Ende einer Zahl sind signifikant, wenn die Zahl eine Dezimalzahl enthält.
Ex. 45,00- Die Nullen in dieser Zahl sind signifikant.
Daher hat es 4 signifikante Stellen.
∙ Nullen am Ende einer Zahl sind signifikant, wenn ein Dezimalpunkt vorhanden ist.
Ex. 12000,- Die Nullen in dieser Zahl sind signifikant. Daher hat es 5 signifikante Stellen.
∙ Nullen am Ende einer Zahl sind nicht signifikant, wenn die Zahl kein Dezimalzeichen enthält.
Ex. 3.400- Die Nullen in dieser Zahl sind nicht signifikant. Daher hat es 2 signifikante Stellen.
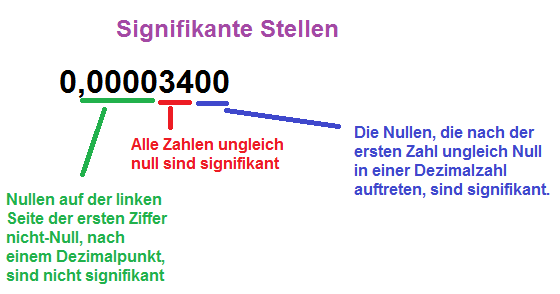
∙ Nullen auf der linken Seite der ersten Ziffer nicht-Null, nach einem Dezimalpunkt, sind nicht signifikant.
Ex. 0,000076- Die Nullen in dieser Zahl sind nicht signifikant. Daher hat es 2 signifikante Stellen.
∙ Die Nullen, die nach der ersten Zahl ungleich Null in einer Dezimalzahl auftreten, sind signifikant.
Ex. 0,0005600- Die ersten 3 Nullen sind nicht signifikant. Die letzten 2 Nullen sind. Daher hat diese Zahl 4 signifikante Stellen.
Dies sind die allgemeinen Regeln für das Wissen, welche Ziffern signifikant sind und welche nicht.
Um diesen Rechner zu benutzen, gibt ein Benutzer einfach eine Zahl ein, für die er die Anzahl der signifikanten Zahlen finden möchte und welche Ziffern der Zahl signifikant sind. Nachdem die Nummer eingegeben wurde, klickt der Benutzer auf die Schaltfläche 'Anzahl der signifikanten Stellen suchen'. Die resultierenden signifikanten Zahlen werden automatisch berechnet.
Elektronik, wie jede andere Wissenschaft, befasst sich mit Messungen, so ist es wichtig zu wissen, wie man mit signifikanten Zahlen umgehen. Je nach verwendetem Messwerkzeug bestimmt, wie genau es messen kann. Die Verwendung der richtigen Anzahl von signifikanten Zahlen kann aus den oben diskutierten Gründen extrem wichtig sein.
Ähnliche Ressourcen
Runden Signifikante Stellen Rechner
Wissenschaftliche Schreibweise Rechner
Faktorisierung Rechner
Konfidenzintervall Rechner
Hypothesentest Rechner
Tschebyscheff-Ungleichung Rechner
Bernoulli Ungleichung Rechner
