Hypothesentest Rechner

Wählen Sie die Art der Hypothesentests: linksseitige (μ < H₀) (einseitig) rechtsseitige (μ > H₀) (einseitig) zweiseitige

Geben Sie die Nullhypothese ein: (H₀):

Geben Sie die Probendurchschnitt ein, x:

Geben Sie die Standardabweichung ein:

Geben Sie die Stichprobengröße ein:

Wählen Sie das Signifikanzniveau: 20% 10% 5% 1% 0,5% 0,1%

Ergebnis:



Dieser Hypothesentest Rechner bestimmt, ob eine alternative Hypothese wahr ist oder nicht. Auf der Grundlage, ob es wahr ist oder nicht, entscheidet, ob die Hypothese akzeptiert oder abgelehnt werden soll. Wir akzeptieren wahre Hypothesen und weisen falsche Hypothesen zurück.

Die Nullhypothese ist die Hypothese, die behauptet wird und die wir testen werden.

Die Alternative Hypothese ist die Hypothese, dass wir glauben, ist tatsächlich wahr.

Zum Beispiel, sagen wir, dass ein Unternehmen behauptet, es erhält nur 20 Verbraucher Beschwerden im Durchschnitt ein Jahr. Jedoch glauben wir, dass es höchstwahrscheinlich viel mehr erhält. In diesem Fall ist die Nullhypothese die behauptete Hypothese der Firma, dass die durchschnittlichen Beschwerden 20 (μ = 20) sind. Die alternative Hypothese ist, dass μ> 20, was wir vermuten. Wenn wir also unsere Tests durchführen, sehen wir, welche Hypothese tatsächlich wahr ist, die Null (behauptet) oder die Alternative (was wir glauben).

Das Signifikanzniveau, das Sie auswählen, bestimmt, wie breit ein Bereich der Ablehnungsbereich sein wird. Das Signifikanzniveau repräsentiert die gesamte Ablehnungsfläche einer normalen Standardkurve. Wenn Sie also mit einem Signifikanzniveau von 1% berechnen, wählen Sie eine normale Standardverteilung mit einer Ablehnungsfläche von 1% der gesamten 100%. Wenn Sie ein Signifikanzniveau von 5% wählen, erhöhen Sie die Abstoßungsfläche auf 5% der 100%. Wenn Sie ein Signifikanzniveau von 20% wählen, erhöhen Sie die Ablehnungsfläche der Standard-Normalkurve auf 20% der 100%. Je mehr Sie das Signifikanzniveau erhöhen, desto größer ist die Ablehnung. Dies bedeutet, dass es eine größere Wahrscheinlichkeit gibt, dass eine Hypothese zurückgewiesen wird und eine engere Chance, die Sie von der Annahme der Hypothese haben, da der Nicht-Ablehnungsbereich abnimmt. Je größer das Signifikanzniveau, desto kleiner oder enger der Nicht-Ablehnungsbereich. Je geringer der Signifikanzpegel, desto größer der Nicht-Ablehnungsbereich.

Es gibt drei Arten von Hypothesen-Tests, die wir tun können.

Es gibt linksseitige, rechtsseitige und zweiseitige Hypothesentests.

Linksseitige Hypothesentest

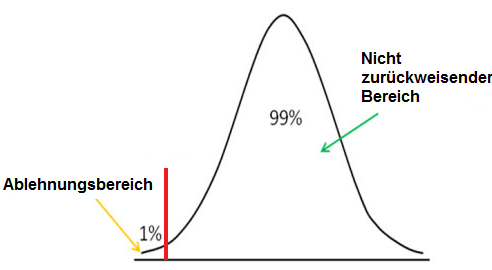
Die linksseitige hypothesentest ist nachstehend dargestellt::

Wir verwenden die linksseitige Hypothesentest, um festzustellen, ob die z-Wert oberhalb des Signifikanzniveaus liegt, in welchem Fall wir die Nullhypothese als wahr akzeptieren.

Die linksseitige Methode hat genau wie die rechtsseitige Methode einen Abreißpunkt. Die von Ihnen gewählte Signifikanzstufe legt diesen Grenzwert fest. Jeder Wert unterhalb dieser Abschneidung in der linksseitigen Methode repräsentiert den Ablehnungsbereich. Dies bedeutet, dass, wenn wir eine z-Wert unter dem Abreißpunkt zu erhalten, wird die z-Score in der Ablehnung Gebiet sein. Dies bedeutet, dass die Hypothese falsch ist. Wenn der z-Wert oberhalb des Abschneidepunkte liegt, bedeutet dies, dass er sich im Nicht-Ablehnungsbereich befindet, und wir nehmen die Hypothese als wahr an.

Die Methode der linksseitigen Hypothese wird verwendet, wenn wir bestimmen wollen, ob ein Stichprobenmittel kleiner als das Hypothesenmittel ist. Zum Beispiel, sagen wir, dass die Hypothese bedeutet, ist $40.000, die die durchschnittliche Gehalt für Sanitäreinrichtungen darstellt, und wir wollen festzustellen, ob dieses Gehalt wurde in den letzten Jahren sank. Das heißt, wir wollen sehen, ob das Stichprobenmittel kleiner ist als das Hypothesenmittel von $40.000. Dies ist ein klassischer linksseitiger Hypothesentest, bei dem die Stichprobe x < H0. Liegt die z-Punktzahl unterhalb des Signifikanzgrenzwertes, so bedeutet dies, dass wir die Hypothese ablehnen, denn die Hypothese ist viel höher als das, was das eigentliche Mittel wirklich ist. Daher ist es falsch und wir lehnen die Hypothese ab. In diesem Fall ist die alternative Hypothese wahr. Liegt der z-Wert oberhalb des Signifikanzgrenzwertes, so bedeutet dies, daß wir die Nullhypothese akzeptieren und die Alternativhypothese ablehnen, die besagt, daß sie geringer ist, weil das wirkliche Mittel wirklich größer ist als das Hypothesenmittel.

Rechtsseitige Hypothesentest

Rechtsseitige Hypothesentest werden nachstehend dargestellt:

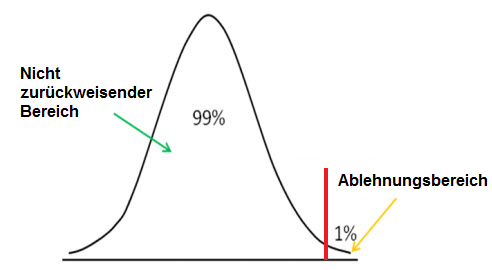
Wir verwenden rechtsseitige Hypothesentests, um zu sehen, ob die z-Wert unter dem Signifikanzniveau-Grenzwert liegt, wobei wir die Nullhypothese als wahr akzeptieren.

Die rechtsseitige Methode hat genau wie die linksseitige Methode einen Abschneidepunkt. Die von Ihnen gewählte Signifikanzstufe legt diesen Grenzwert fest. Jeder Wert oberhalb dieses Abschneidepunkte in der rechten Schwanzmethode stellt den Abstoßungsbereich dar. Dies bedeutet, dass, wenn wir einen z-Wert über dem Abschneidepunkte zu erhalten, wird die z-Score in der Zurückweisung Bereich sein. Dies bedeutet, dass der Nullhypothesenanspruch falsch ist. Wenn der z-Wert unter dem Abschneidepunkte liegt, bedeutet dies, dass er sich im Nicht-Ablehnungsbereich befindet, und wir nehmen die Hypothese als wahr an.

Die rechtsseitige Methode wird verwendet, wenn ermittelt werden soll, ob ein Stichprobenmittel größer als das Hypothesenmittel ist. Zum Beispiel, sagen wir, dass ein Unternehmen behauptet, dass es 400 Arbeiter Unfälle pro Jahr. Dies bedeutet, dass die Nullhypothese 400 ist. Wir vermuten jedoch, dass es viel mehr Unfälle als dies hat. Daher wollen wir feststellen, ob diese Anzahl von Unfällen größer ist als das, was behauptet wird. Das heißt, wir wollen sehen, ob das Stichprobenmittel größer ist als das Hypothesenmittel von 400. Dies ist ein klassischer rechtsseitiger Hypothesentest, bei dem die Stichprobe x > H0 ist. Dies ist die alternative Hypothese. Die Nullhypothese ist, dass das Mittel 400 Arbeiterunfälle pro Jahr ist. Und die alternative Hypothese ist, dass das Mittel größer als 400 Unfälle pro Jahr ist. Wenn der berechnete z-Wert über dem Signifikanzniveau-Grenzwert liegt, bedeutet dies, dass wir die Nullhypothese ablehnen und die Alternativhypothese akzeptieren, weil die Hypothese wesentlich niedriger ist als das, was das wirkliche Mittel wirklich ist. Daher ist es falsch und die alternative Hypothese ist wahr. Das bedeutet, dass es jährlich mehr als 400 Arbeitsunfälle gibt und der Anspruch des Unternehmens ungenau ist. Liegt der z-Wert unterhalb des Signifikanzgrenzwertes, so bedeutet dies, dass wir die Nullhypothese akzeptieren und die alternative Hypothese ablehnen, die besagt, dass sie mehr ist, weil das eigentliche Mittel tatsächlich kleiner ist als das Hypothesenmittel. Dies bedeutet wirklich, es gibt weniger als 400 Arbeiter Unfälle pro Jahr und der Anspruch des Unternehmens ist richtig.

Zweiseitige Hypothesentest

Zweiseitige Hypothesentest werden nachstehend dargestellt:

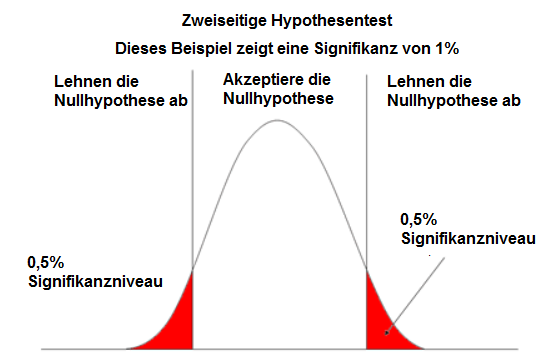
Wir verwenden die zweiseitige Methode, um zu sehen, ob der tatsächliche Stichprobenmittelwert nicht gleich dem ist, was im Hypothesenmittel behauptet wird.

Also, wenn das Hypothesenmittel mit 100 behauptet wird. Die alternative Hypothese kann behaupten, dass das Stichprobenmittel nicht 100 ist.

Die zweiseitige Methode hat 2 Abschneidepunkte. Die von Ihnen gewählte Signifikanzstufe legt diese Grenzwerte fest. Wenn Sie ein Signifikanzniveau von 1% wählen, werden die 2 Enden der Normalkurve jeweils 0,5% umfassen, um die volle 1% Signifikanz zu bilden. Wenn Sie ein Signifikanzniveau von 5% wählen, werden die 2 Enden der Normalkurve jeweils 2,5% umfassen, um die Enden zu bilden.

Wenn der berechnete z-Wert zwischen den beiden Enden liegt, nehmen wir die Nullhypothese an und lehnen die alternative Hypothese ab. Dies liegt daran, dass der z-Wert im Nicht-Ablehnungsbereich liegt. Liegt der z-Wert außerhalb dieses Bereichs, dann lehnen wir die Nullhypothese ab und akzeptieren die Alternative, weil sie außerhalb des Bereichs liegt. Daher ist das Probenmittel tatsächlich von dem Nullhypothesenmittel verschieden, was der beanspruchte Mittelwert ist.

Um diesen Rechner zu verwenden, wählt ein Benutzer das Nullhypothesenmittel (den beanspruchten Mittelwert), den Stichprobenmittelwert, die Standardabweichung, die Stichprobengröße und das Signifikanzniveau aus und klickt auf die Schaltfläche "Berechnen". Die resultierende Antwort wird automatisch berechnet und unten gezeigt, mit einer Erklärung zur Antwort.

Hypothesen-Tests können für jede Art von Wissenschaft verwendet werden, um zu zeigen, ob wir ablehnen oder akzeptieren eine Hypothese auf der Grundlage von quantitativen Computing. Selbst in bestimmten Bereichen der Elektronik, könnte es nützlich sein.

Ähnliche Ressourcen

Konfidenzintervall Rechner

Tschebyscheff-Ungleichung Rechner

Bernoulli Ungleichung Rechner

Signifikante Stellen Rechner

Runden Signifikante Stellen Rechner

Wissenschaftliche Schreibweise Rechner

Faktorisierung Rechner

Korrelationskoeffizient Rechner

Gleichungssystem Rechner