Calculatrice de Factorisation

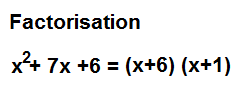
Le calculateur de factorisation calcule les facteurs qui comprennent un polynôme.
Cette calculatrice traite exclusivement des binômes et trinomials. Il ne calcule pas les facteurs de tout autre type de polynôme.
Un binôme est un polynôme qui contient 2 termes. Des exemples de binômes sont x2-36, 2x2-40, and x2-100.
Un trinomial est un polynôme qui contient 3 termes. Des exemples de trinomials sont x2 +3x +2, 2x2-14x-7, and 72+5x-14.
Ce calculateur calcule le facteur des polynômes du 2ème degré, ce qui signifie que le plus haut exposant x est le deuxième degré. Il ne dépasse pas le 2ème degré. Par conséquent, il ne calcule pas les cubes ou les exposants au-dessus de 2.
D'autres choses importantes à connaître sur cette calculatrice sont la variable doit être x dans l'expression. C'est la seule variable que la calculatrice reconnaît.
L'expression sera toujours prise en compte si l'expression peut être prise en compte, mais elle ne doit pas toujours être complètement réduite. Cette calculatrice est un calculateur de factorisation principalement, pas réducteur.
Ce calculateur de factorisation calcule les facteurs qui comprennent un polynôme via un certain nombre de méthodes.
Une méthode commune qui est faite est que la calculatrice examine tous les termes du polynôme.
Il est plus facile de visualiser avec ceci avec un exemple réel, alors nous allons regarder un exemple maintenant.
x2 + 11x + 24
Ainsi, dans cet exemple, le premier terme est 1 et le dernier terme est 24. La calculatrice multipliera ces termes pour obtenir la valeur de 24. Cette valeur de 24 est très importante car elle représente le dernier terme d'un polynôme. Ainsi, une fois que nous obtenons cette valeur de 24, la calculatrice examine tous les facteurs de 24, qui sont {1,24}, {2, 12}, {3,8} et {4,6}. La calculatrice examine alors le terme à moyen terme. Il voit si l'un ou l'autre des facteurs s'élève au terme à moyen terme. Si l'un des facteurs le font, c'est un match. Et ce sont les facteurs qui composent le polynôme. Donc dans ce cas, les facteurs sont 3 et 8. Donc, la réponse finale est (x + 3)(x + 8).
C'est le cas si toutes les valeurs sont positives.
Examinons maintenant un exemple où tous les nombres ne sont pas positifs et voir comment ce calculateur modifie.
Nous utiliserons donc des valeurs similaires au polynôme ci-dessus, mais rendons le dernier terme négatif.
x2 -5x - 24
Donc, maintenant, le premier terme est 1 et le dernier terme est -24. Ceci produit un produit de -24. Encore une fois, nous utilisons les facteurs de 24 qui sont {1,24}, {2, 12}, {3,8} et {4,6}. Étant donné que cela est négatif, cela implique que l'un des termes est négatif et l'autre positif, puisque la seule façon d'obtenir un résultat négatif est positive et négative. Donc, quand un facteur est négatif et l'autre positif, les chiffres n'ajoutent pas, mais restent totalement. Par conséquent, lorsque le dernier terme est négatif, comme dans ce cas, le terme moyen est la différence entre les facteurs correspondants. Étant donné que le terme moyen est -5 dans ce cas, les facteurs sont -8 et 3. Donc, la réponse finale est (x-8)(x+3).
Il s'agit d'une méthode que la calculatrice utilise pour calculer les facteurs d'un polynôme.
Cependant, cette méthode n'attrapera pas toutes les valeurs.
La méthode de l'étalon-or des facteurs informatiques se fait via le calcul de la formule quadratique.
En utilisant la formule quadratique ci-dessous, nous pouvons calculer les facteurs qui constituent un polynôme.
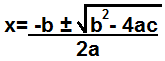
La formule quadratique calcule les 2 facteurs qui constituent un polynôme.
Si les résultats de la formule quadratique apparaissent comme des nombres entiers, le polynôme peut être pris en compte. Si les résultats apparaissent sous forme de nombres fractionnés, le polynôme peut être pris en compte selon la valeur du coefficient du premier. Si les résultats ne peuvent ni des nombres entiers ni des fractions, le polynôme ne peut pas être pris en compte.
Un exemple d'un polynôme dans lequel la formule quadratique produit des nombres entiers est présenté ci-dessous.
x2 + 20x + 21
La résolution de l'équation quadratique donne les facteurs de x = -1 et x = -20. Ces deux facteurs sont des nombres entiers.
Ainsi, la factorisation final du polynôme donne la réponse de (x+1)(x+20).
Un exemple d'un polynôme dans lequel la formule quadratique produit des nombres fractionnaires est présenté ci-dessous.
18x2 +54x +28
La résolution de l'équation quadratique donne les facteurs de x= -2 1/3 et x = -2/3.
Mais ce n'est pas la dernière réponse. Notez comment le coefficient avant le premier terme est de 18. Si nous divisons 18 dans les facteurs 6 et 3, nous pouvons multiplier ces facteurs par les valeurs obtenues dans la formule quadratique pour produire des nombres entiers. 6 * -2 1/3 = -14, donc un facteur est -14. 3* -2/3 = -2, donc l'autre facteur est -2. Ceci produit le résultat final de (6x+14)(3x+2).
Un exemple d'un polynôme qui produit des résultats qui ne sont ni entiers ni fractionnels est présenté ci-dessous.
6x2 + 8x +4
La formule quadratique de cette équation ne peut être résolue. Ainsi, cette équation ne peut être prise en compte.
C'est parce que lors de la résolution de la formule quadratique dans la racine carrée, le nombre est négatif.
La racine carrée pour un nombre négatif est indéfinie, donc l'équation ne peut pas être résolue.
Ainsi, vous pouvez voir l'importance de la formule quadratique et la façon dont elle est utilisée pour trouver les facteurs d'un polynôme (si la factorisation est possible).
Par conséquent, ce calculateur utilise lourdement la formule quadratique pour calculer si le polynôme est factorisable ou non.
Ressources Connexes
Calculatrice de Chiffres Significatifs
Calculatrice d'Arrondi des Chiffres Significatifs
Calculatrice de Notation Scientifique
Calculatrice de L'inégalité de Bienaymé-Tchebychev
Calculatrice de L'inégalité de Bernoulli
Calculatrice de L'intervalle de Confiance
Calculatrice de Test d'Hypothèse Statistique
