Binomial Coefficient Calculator

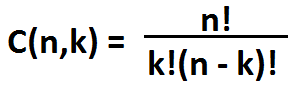
This Binomial Coefficient Calculator calculates the number of ways of picking k unordered outcomes from n possibilities.

n represents the total sample space. The sample space is the total number of items.

k represents the number items chosen from the sample space.

The result, the binomial coefficient, represents the number of unordered outcomes we can selecting k terms from a total sample space of n terms.

The formula for calculating the binomial coefficient is C(n,k) = n!/(k!(n-k)!). We take the factorial of n and divide it by the factorial of k and (n - k).

Being that the formula involves taking the factorial of our input terms, only nonnegative integer values can be entered into the calculator. If a negative number or decimal are entered into the calculator, an error message will appear.

To show an example of binomial coefficient computation, we'll given an example. Let's say we have a total of 10 balloons and each balloon is a different color. And let's say we can only select 3 of the balloons from the 10. How many different combinations of balloons can we have?

This is a combination problem. We use the formula above. n=10 and k=3. Plugging the values into the formula, we get the resultant value of 120. This means there are 210 unordered possibilities of arranging 3 balloons from a total of 10 balloons.

To use this calculator, a user simply enters in the n and k values and clicks the 'Calculate' button. The resultant value, the binomial coefficient, will be computed and displayed.

Examples

Find the binomial coefficient if n=10 and k=4.

Answer:

C(n,k) = n!/(k!(n-k)!)= 10!/(4! * 6!) = 210

So the binomial coefficient is 210.

This means there are 210 ways we can arrange 4 items from a set of 10 items.

Find the binomial coefficient if n=20 and k=3.

Answer:

C(n,k) = n!/(k!(n-k)!)= 20!/(3! * 17!) = 1140

So the binomial coefficient is 1140.

This means there are 1140 ways we can arrange 3 items from a set of 20 items.

Related Resources

Variance Calculator

Standard Deviation Calculator

Expected Value Calculator

Z Score Calculator

Z Score to Raw Score Calculator

Chebyshev's Theorem Calculator

System of Equations Calculator

Factorial Calculator

Significant Figures (Sig Fig) Calculator

Hypothesis Testing Calculator