Expected Value Calculator
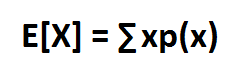
This Expected Value Calculator calculates the expected value of a number or set of numbers based on the probability of that number or numbers occurring.
The expected value is the value which you would expect to receive for a future average or mean in advance.
The formula for expected value for a set of numbers is the value of each number multiplied by the probability of each value occurring. This formula, in mathematical terms, is represented by ∑xp(x). This formula states that for each x value in a group of numbers, if we multiply each x value by the probability of that value occurring, we will have calculated the expected value.
Being that the expected value measures the expected outcome of the probabilities of a set of number, the individual probabilities must collectively add up to 1 or 100%. Also, none of the probabilities for any of the events can be greater than 1. This is because the probability of an event happening cannot be greater than 100%. Therefore, the calculator will display an error message if either any of the events has a probability greater than 1 or if the individual probabilities do not add up to 1 or 100%. 100% is the total possible outcome. So there is no way an event or all the events totaled can have a probability of greater than 1.
To get a more practical illustration of expected value, let's go through a real-world example.
The example we will go over is a money show. Let's say we have a show and the contestants spin a wheel for to win money. The wheel can choose 1 of 10 numbers, from 1 to 10. If the contestant spins and the number is 9, he will win $10,000. If he spins and spinner stops at 2, he will $5,000. For all other numbers, he will win $2000. This means he's guaranteed to win $2000, may win $5000, and may win $10,000.
Since there are 10 numbers and only the 9 will $10,000, there is a 10%, or 0.1, chance of him winning $10,000. For the same reason, since there are 10 numbers and only the 2 will win $5,000, there, again is a 10% chance he will win $5000. For the other 8 numbers, he will win $2000. So there is an 80%, or 0.8, chance of him winning $2000. What is the expected value for this group of numbers?
The table below represents the information above:
| X | $10,000 | $5,000 | $2,000 |
| P(X) | 10% or 0.1 | 10% or 0.1 | 80% or 0.8 |
The expected value of the number set will be the value of each x times the probability of each occurring.
So the expected value will be equal to ∑xp(x)= $10,000(0.1) + $5,000(0.1) + $2,000(0.8)= $3,100.
This $3,100 means that on average, for the future spins, $3,100 is the average that is usually found. In this way, you can see that the expected value is the future mean or mean in advance. Using the probability of each event occurring, it allows us to predict, on average, what the average outcome will be, based on a good number of events occurring.
The expected value is very important because it is a tool that allows us to predict future outcomes, such as the game show money winning we just went over.
We can apply the expected value into all areas of math and science to help gauge future outcomes.
To use this calculator, a user simply enters in the value of each event and the probability of each event occurring.
The probability can be entered in either in
percent form or in decimal form. If using percent form, the user must add the percent sign (%) at the end of the number. Or
else, the calculator will assume the number is in decimal form. A user does not have to use up all 10, just as many
as he or she needs. After, the user clicks the 'Calculate' and the expected value will be calculated and automatically displayed.
Related Resources
Variance Calculator
Standard Deviation Calculator
Expected Value Calculator
Z Score Calculator
Z Score to Raw Score Calculator
Chebyshev's Theorem Calculator
Binomial Coefficient Calculator
Bernoulli Trial Calculator
Area Under the Curve Calculator
Confidence Interval Calculator
Sample Correlation Coefficient Calculator
Regression Line Calculator
Slope and y-intercept of a Regression Line Calculator
Test Statistic Calculator
Paired t-test Calculator
Unpaired t-test Calculator
T-value Calculator
Sample Size Calculator
Margin of Error Calculator
