Hypothesis Testing Calculator

Select the type of Hypothesis Testing: Left-tail (μ < H₀) (One tail) Right-tail (μ > H₀) (One tail) Two tail

Enter the Null Hypothesis (H₀) Mean:

Enter the Sample Mean, x:

Enter the Standard Deviation:

Enter the Sample Size:

Select the Significance Value: 20% 10% 5% 1% 0.5% 0.1%

Result:



This Hypothesis Testing Calculator determines whether an alternative hypothesis is true or not. Based on whether it is true or not determines whether we accept or reject the hypothesis. We accept true hypotheses and reject false hypotheses.

The null hypothesis is the hypothesis that is claimed and that we will test against.

The alternative hypothesis is the hypothesis that we believe it actually is.

For example, let's say that a company claims it only receives 20 consumer complaints on average a year. However, we believe that most likely it receives much more. In this case, the null hypothesis is the claimed hypothesis by the company, that the average complaints is 20 (μ=20). The alternative hypothesis is that μ > 20, which is what we suspect. So when we do our testing, we see which hypothesis is actually true, the null (claimed) or the alternative (what we believe it is).

The significance level that you select will determine how broad of an area the rejection area will be. The significance level represents the total rejection area of a normal standard curve. Therefore, if you choose to calculate with a significance level of 1%, you are choosing a normal standard distribution that has a rejection area of 1% of the total 100%. If you choose a significance level of 5%, you are increasing the rejection area to 5% of the 100%. If you choose a significance level of 20%, you increase the rejection area of the standard normal curve to 20% of the 100%. The more you increase the significance level, the greater area of rejection there is. This means that there is a greater chance a hypothesis will be rejected and a narrower chance you have of accepting the hypothesis, since the nonrejection area decreases. So the greater the significance level, the smaller or narrower the nonrejection area. The smaller the significance level, the greater the nonrejection area.

There are 3 types of hypothesis testing that we can do.

There is left tail, right tail, and two tail hypothesis testing.

Left Tail

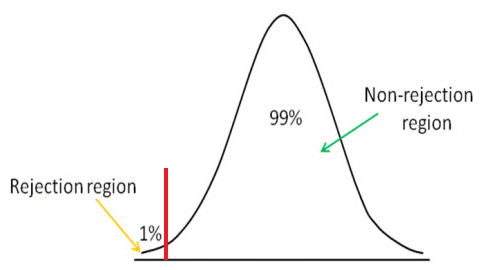
Left tail hypothesis testing is illustrated below:

We use left tail hypothesis testing to see if the z score is above the significance level critical value, in which case we cannot reject the hypothesis.

The left tail method, just like the right tail, has a cutoff point. The significance level that you choose determines this cutoff point called the critical value. Any value below this critical value in the left tail method represents the rejection area. This means that if we obtain a z score below the critical value, the z score will be in the rejection area. This means that the hypothesis is false. If the z score is above the critical value, this means that it is is in the nonrejection area, and we cannot reject the hypothesis.

The left tail method is used if we want to determine if a sample mean is less than the hypothesis mean. For example, let's say that the hypothesis mean is $40,000, which represents the average salary for sanitation workers, and we want to determine if this salary has been decreasing over the last few years. This means we want to see if the sample mean is less than the hypothesis mean of $40,000. This is a classic left tail hypothesis test, where the sample mean, x < H0. If the z score is below the critical value, this means that we reject the hypothesis, because the hypothesis mean is much higher than what the real mean really is. Therefore, it is false and we reject the hypothesis. In this case, the alternative hypothesis is true. If the z score is above the critical value, this means that we cannot reject the null hypothesis and we reject the alternative hypothesis which states it is less, because the real mean is really greater than the hypothesis mean.

Right Tail

Right tail hypothesis testing is illustrated below:

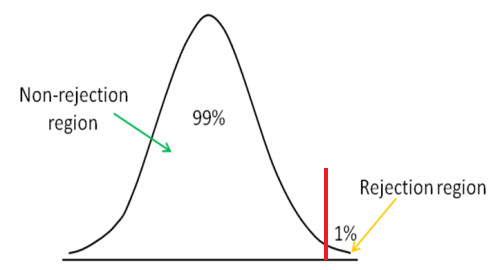
We use right tail hypothesis testing to see if the z score is below the significance level critical value, in which case we cannot reject the null hypothesis as true.

The right tail method, just like the left tail, has a critical value. The significance level that you choose determines this critical value point. Any value above this critical value in the right tail method represents the rejection area. This means that if we obtain a z score above the critical value, the z score will be in the rejection area. This means that the null hypothesis claim is false. If the z score is below the critical value, this means that it is is in the nonrejection area, and we cannot reject the hypothesis.

The right tail method is used if we want to determine if a sample mean is greater than the hypothesis mean. For example, let's say that a company claims that it has 400 worker accidents a year. This means that the null hypothesis is 400. However, we suspect that is has much more accidents than this. Therefore, we want to determine if this number of accidents is greater than what is being claimed. This means we want to see if the sample mean is greater than the hypothesis mean of 400. This is a classic right tail hypothesis test, where the sample mean, x > H0. This is the alternative hypothesis. The null hypothesis is that the mean is 400 worker accidents per year. And the alternative hypothesis is that the mean is greater than 400 accidents a year. If the z score calculated is above the critical value, this means that we reject the null hypothesis and accept the alternative hypothesis, because the hypothesis mean is much lower than what the real mean really is. Therefore, it is false and the alternative hypothesis is true. This means that there really more than 400 worker accidents a year and the company's claim is inaccurate. If the z score is below the critical value, this means that we cannot reject the null hypothesis and we reject the alternative hypothesis which states it is more, because the real mean is actually less than the hypothesis mean. This really means there are fewer than 400 worker accidents a year and the company's claim is correct.

Two Tail

Two tail hypothesis testing is illustrated below:

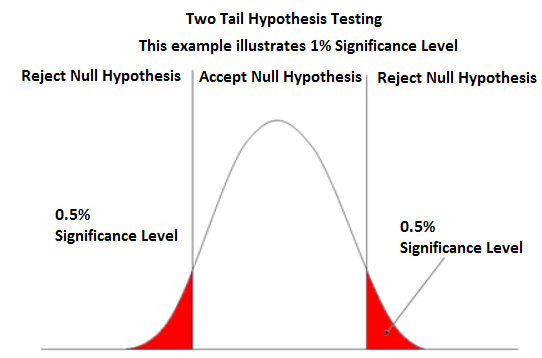
We use the two tail method to see if the actual sample mean is not equal to what is claimed in the hypothesis mean.

So if the hypothesis mean is claimed to be 100. The alternative hypothesis may claim that the sample mean is not 100.

The two tail method has 2 critical values (cutoff points). The significance level that you choose determines these critical value points. If you choose a significance level of 1%, the 2 ends of the normal curve will each comprise 0.5% to make up the full 1% significance level. If you choose a significance level of 5%, the 2 ends of the normal curve will each comprise 2.5% to make up the ends.

If the calculated z score is between the 2 ends, we cannot reject the null hypothesis and we reject the alternative hypothesis. This is because the z score will be in the nonrejection area. If the z score is outside of this range, then we reject the null hypothesis and accept the alternative hypothesis because it is outside the range. Therefore, the sample mean is actually different from the null hypothesis mean, which is the mean that is claimed.

To use this calculator, a user selects the null hypothesis mean (the mean which is claimed), the sample mean, the standard deviation, the sample size, and the significance level and clicks the 'Calculate' button. The resultant answer will be automatically computed and shown below, with an explanation as to the answer.

Hypothesis testing can be used for any type of science to show whether we reject or accept a hypothesis based on quantitative computing. Even in certain areas of electronics, it could be useful.

Related Resources

Test Statistic Calculator

Paired t-test Calculator

Unpaired t-test Calculator

T-value Calculator

p-value Calculator

Variance Calculator

Standard Deviation Calculator

Expected Value Calculator

Z Score Calculator

Z Score to Raw Score Calculator

Chebyshev's Theorem Calculator

Binomial Coefficient Calculator

Bernoulli Trial Calculator

Area Under the Curve Calculator

Confidence Interval Calculator

Sample Correlation Coefficient Calculator

Sample Size Calculator

Significant Figures (Sig Fig) Calculator