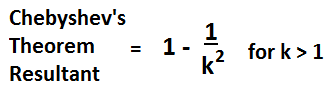Chebyshev's theorem is a theorem that allows us to approximately know how much percentage of a data set lies within a certain number of standard deviations of the mean of the data set.
The mathematical equation to compute Chebyshev's theorem is shown below.
Chebyshev's theorem states for any k > 1, at least 1-1/k2 of the data lies within k standard deviations of the mean.
As stated, the value of k must be greater than 1.
Using this formula and plugging in the value 2, we get a resultant value of 1-1/22, which is equal to 75%. This means that at least 75% of the data for a set of numbers lies within 2 standard deviations of the mean. The number could be greater. It could be all, 100%, but it's guaranteed to be at least 75%. And this is what Chebyshev's theorem computes.
If we plug in 3 for k, then the resultant value is 88.89%. This means that at least 88.89% of a data set lies within 3 standard deviations of the mean.
If we plug in 4 for k, then the resultant value is 93.75%. This means that at least 93.75% of a data set lies within 3 standard deviations of the mean.
Chebyshev's theorem is a great tool to find out how approximately how much percentage of a population lies within a certain amount of standard deviations above or below a mean. It tells us at least how much percentage of the data set must fall within that number of standard deviations.
To use this calculator, a user simply enters in a k value. This k value represents the number of standard deviations from the mean.
The resultant value calculated will represent the minimum percentage of the data set that falls within k standard deviations of the mean.
Chebyshev's theorem is a great statistical measure because it can be used in electronics math for various statistical purposes.
Related Resources
Test Statistic Calculator
Paired t-test Calculator
Unpaired t-test Calculator
T-value Calculator
p-value Calculator
Confidence Interval Calculator
Dot Product Calculator
FOIL Calculator- Multiplying Binomials
Exponential Calculator
How to Convert Degrees to Radians
How to Convert Radians to Degrees
Degrees to Radians Calculator
Radians to Degrees Calculator
Ratio Calculator
Expected Value Calculator