Confidence Interval Calculator
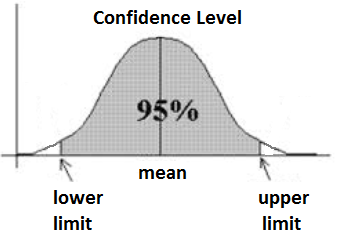
This Confidence Interval Calculator calculates the confidence interval for group of data, given we have the mean, standard deviation, and sample size for the data unit.
The confidence interval allows us to quantify how confident we can feel a group of data is from its mean value.
This calculator allows us to calculate the confidence interval for a group of data for 50%, 60%, 70%, 80%, 90%, 95%, 98%, 99%, 99.8%, and 99.9% confidence levels.
For example, let's say we have a sample size of 32, with a mean of 33.4 and a standard deviation of 42. We want to calculate the 95% confidence interval for this data. If we do so, we will get the interval of 18.9 to 47.9. This means that we are 95% confident that the mean is between 18.9 and 47.9.
A confidence level of 50% will yield the shortest interval because it is the smallest and the least precise of all the confidence levels. As we increase the confidence level, we get a larger range of values to increase our confidence that the mean will be in the subset. Therefore, as we increase the confidence level, we get a larger and larger range. The confidence interval of 99.9% will yield the largest range of all the confidence intervals.
The confidence interval calculator calculates the confidence interval by taking the standard deviation and dividing it by the square root of the
sample size, according to the formula, σ
Once we obtain this value, we calculate the upper estimate of the interval by the formula, upper estimate= mean + (standard deviation)(value of t α). The value of tα is obtained by looking up the value based on a table. We calculate the lower estimate by the formula, lower estimate= mean - (standard deviation)(value of tα).
To use this calculator, a user simply enters in the mean, standard deviation, the sample size of the data, and the confidence interval s/he wants to find out, and clicks the 'Calculate' button. The resultant confidence interval will be computed and displayed.
Calculating the confidence interval for a given group can be useful for any science, including electronics.
Example
Calculate the 95% confidence interval for a data set given its mean cost is $193.73, its standard deviation is $26.73, and its sample size is 25.
σ
Since the sample size is small (below 30), we take the sample size and subtract 1 to get the degrees of freedom (df). So n -1= 25= 24. If we look up the tα value for 24 with a confidence level of 95, we obtain the value of 2.064.
Upper estimate= 193.32 + (2.064)(5.35)= 204.36
Lower estimate= 193.32 - (2.064)(5.35)= 182.28
So we can be 95% confident that the mean cost for the item will be between $182.28 and $204.56.
Related Resources
Test Statistic Calculator
Paired t-test Calculator
Unpaired t-test Calculator
T-value Calculator
p-value Calculator
Variance Calculator
Standard Deviation Calculator
Expected Value Calculator
Z Score Calculator
Z Score to Raw Score Calculator
Chebyshev's Theorem Calculator
Binomial Coefficient Calculator
Bernoulli Trial Calculator
Area Under the Curve Calculator
Hypothesis Testing Calculator
Sample Correlation Coefficient Calculator
Regression Line Calculator
Slope and y-intercept of a Regression Line Calculator
Sample Size Calculator
Margin of Error Calculator
