Margin of Error Calculator

Margin of Error for the Sample Mean Calculator

The Margin of Error for the Sample Mean Calculator calculates the margin of error based on the confidence level, population standard deviation, and the sample size.
The margin of error (MOE) is the level of error that you are willing to tolerate for a given data set.
The margin of error can be expressed as a decimal or as a percentage.
The formula in order to determine the margin of error is, MOE= ((z * σ)/√
In this formula, z is the z value obtained from the Z distribution table. σ is the population standard deviation of the data set. n is the sample size of the data set.
So looking at this formula, let's analyze it a bit.
When you need a high level of confidence, you have to increase the z-value which, in turn, increases the margin of error; this is bad because a low of margin of error is desired. However, this can be offset by increasing the sample size, which decreases the margin of error. If you choose a low confidence level such as 50%, then this equates to a low z value, which decreases the margin of error. So a high confidence level increases the margin of error. And a low confidence level decreases the margin of error.
And according to the formula, that there is an inverse relationship between the sample size and the margin of error. If we increase the sample size, we decrease the margin of error.
Also, with the population standard deviation, σ, there is a direct relationship with the margin of error. So if we increase the standard deviation value, then we increase the margin of error. If there is a low standard deviation, this decreases the margin of error.
So let's now go over an example.
Let's say we have a confidence interval of 90%, a population standard deviation of 2.8, and a sample size of 400. How can we calculate the margin of error?
So let's go back to the formula, which is,
MOE= ((z * σ)/√
One thing you may notice is that the formula has a z value in it. However, you don't input a z value. The calculator gets the z value from the z distribution table. This value is calculated from the confidence level desired. This calculator allows a user to enter in the confidence levels of 50%, 60%, 70%, 80%, 90%, 95%, 99%, 99.8%, and 99.9%.
A confidence level of 95%, in our example, has a z value of 1.645.
Calculating the value gives us, MOE= ((z * σ)/√
And this is how you can calculate the margin of error for a sample mean, based on the confidence level, population standard deviation, and the sample size.
To use this calculator, a user simply has to enter in the confidence level desired, the population standard deviation, and the sample size
and then click the 'Calculate' button. The resultant margin of error value will then be automatically calculated and displayed.
Margin of Error for the Sample Proportion Calculator
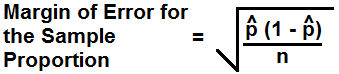
The Margin Error for the Sample Proportion Calculator calculates the amount by which you expect your sample proportion to vary from sample to sample.
So population deals with the whole population (every individual or unit) and a sample is just a portion of the population.
The formula for the margin of error for the sample proportion is, MOE= Z * √p(1-p)/n
p is the sample proportion of the data set.
n is the sample size of the data set.
Thus, all we need to know to compute the margin of error for a sample proportion is the sample proportion and the sample size.
Let's say out of 1000 people, we take a random sample of 800 people. These 800 report reading a book every night for an hour before going to bed. What is the margin of error for this sample proportion if we want to see a 99.9% confidence level?
So the sample proportion, p= 750/1000= .75
The z value for a 99.9% confidence level is, z= 3.291
Therefore, solving the equation, we get, MOE= Z* √.8(1-.8)/1000= Z* √(.16)/1000= Z* √
Thus, to use this calculator, a user simply needs to enter in the confidence level, sample proportion, and the sample size and click the
'Calculate' button. The resultant margin of error value will be automatically computed and shown.
Related Resources
Test Statistic Calculator
Paired t-test Calculator
Unpaired t-test Calculator
Confidence Interval Calculator
Dot Product Calculator
FOIL Calculator- Multiplying Binomials
Exponential Calculator
How to Convert Degrees to Radians
How to Convert Radians to Degrees
Degrees to Radians Calculator
Radians to Degrees Calculator
Ratio Calculator
Expected Value Calculator
