Calculadora de Valor Esperado
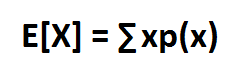
Esta calculadora de valor esperado calcula el valor esperado de un número o conjunto de números basado en la probabilidad de que ese número o números ocurran.
El valor esperado es el valor que esperaría recibir para un promedio futuro o un promedio por adelantado.
La fórmula del valor esperado para un conjunto de números es el valor de cada número multiplicado por la probabilidad de que se produzca cada valor. Esta fórmula, en términos matemáticos, está representada por Σxp(x). Esta fórmula establece que para cada valor de x en un grupo de números, si multiplicamos cada valor de x por la probabilidad de que ocurra ese valor, habremos calculado el valor esperado.
Siendo que el valor esperado mide el resultado esperado de las probabilidades de un conjunto de números, las probabilidades individuales deben agregar colectivamente 1 o 100%. Además, ninguna de las probabilidades para ninguno de los eventos puede ser mayor que 1. Esto se debe a que la probabilidad de que ocurra un evento no puede ser mayor que 100%. Por lo tanto, la calculadora mostrará un mensaje de error si cualquiera de los eventos tiene una probabilidad mayor que 1 o si las probabilidades individuales no suman 1 o 100%. 100% es el resultado total posible. Así que no hay forma en que un evento o todos los eventos sumarizados puedan tener una probabilidad mayor que 1.
Para obtener una ilustración más práctica del valor esperado, vamos a pasar por un ejemplo del mundo real.
El ejemplo que vamos a pasar es un espectáculo de dinero. Digamos que tenemos un espectáculo y los concursantes giran una rueda para ganar dinero. La rueda puede elegir 1 de 10 números, de 1 a 10. Si el competidor gira y el número es 9, ganará $10.000. Si gira y el hilandero se detiene a las 2, tendrá $5.000. Para todos los demás números, ganará $2.000. Esto significa que él está garantizado para ganar $2.000, puede ganar $5.000, y puede ganar $10.000.
Dado que hay 10 números y sólo el 9 obtiene $10.000, hay una probabilidad del 10%, o 0.1, de que gane $10.000. Por la misma razón, ya que hay 10 números y sólo los 2 ganarán $5.000, allí, de nuevo es un 10% de probabilidad de que gane $5.000. Para los otros 8 números, ganará $2.000. Así que hay una probabilidad del 80%, o 0.8, de que él gane $2.000. ¿Cuál es el valor esperado para este grupo de números?
La siguiente tabla muestra la información anterior:
| X | $10.000 | $5.000 | $2.000 |
| P(X) | 10% or 0,1 | 10% or 0,1 | 80% or 0,8 |
El valor esperado del conjunto de números será el valor de cada x multiplicado por la probabilidad de que cada uno ocurra.
Por lo tanto, el valor esperado será igual a ∑xp(x)= $10.000(0,1) + $5.000(0,1) + $2.000(0,8)= $3.100.
Este $ 3,100 significa que en promedio, para las vueltas futuras, $3.100 es el promedio que se encuentra generalmente. De esta manera, puede ver que el valor esperado es la media futura o la media por adelante. Usando la probabilidad de que ocurra cada evento, nos permite predecir, en promedio, cuál será el resultado promedio, basado en un buen número de eventos que ocurren.
El valor esperado es muy importante porque es una herramienta que nos permite predecir los resultados futuros, como el ejemplo de ganar dinero en un juego.
Podemos aplicar el valor esperado en todas las áreas de matemáticas y ciencias para ayudar a medir los resultados futuros.
Para usar esta calculadora, un usuario simplemente ingresa el valor de cada evento y la probabilidad de que ocurra cada evento. La probabilidad se puede introducir en
en forma de porcentaje o en forma decimal. Si utiliza el formulario de porcentaje, el usuario debe agregar el signo de porcentaje (%) al final del número. O bien, la calculadora asumirá que el número está en forma decimal. Un usuario no tiene que usar todos los 10, tanto como él o ella necesita. Después, el usuario hace clic en 'Calcular' y el valor esperado se calculará y se mostrará automáticamente.
Recursos Relacionados
Calculadora de Teorema de Chebyshev
Calculadora de Intervalo de Confianza
Calculadora de Prueba de Hipótesis Estadística
Calculadora de Cifras Significativas
Calculadora del Redondeo de Cifras Significativas
Calculadora de Prueba T de Student
Calculadora de Prueba T para Muestras Relacionadas
Calculadora de Prueba T para Muestras Independientes
Calculadora de Valor de p
