Calculadora de Prueba T de Student
Calculadora de Prueba T para Muestra Única
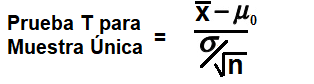
La calculadora de prueba T para Muestra Única es una calculadora que se usa cuando la variable es numérica y solo se está estudiando una población o grupo.
Digamos que un economista, el economista William German, cree que los estudiantes que trabajan e ingresan a la universidad solo gastan, en promedio, $15 por día en comida. La variable, dinero, es numérica y la población son todos los estudiantes que trabajan e ingresan a la universidad.
La hipótesis nula en este ejemplo para este economista es, H0= μ = $15. μ representa la cantidad promedio de dinero en dólares que todos los estudiantes universitarios que trabajan pasan un día comiendo. El economista afirma que este monto promedio es igual a $ 15.
La hipótesis alternativa, Ha, es μ > 15, μ < 15 o μ ≠ 15. En este ejemplo, diremos que Ha es igual a $20 por día. Entonces, la hipótesis alternativa es que los estudiantes universitarios que trabajan realmente gastan $20 por día en comida en lugar de los $15 que cree el economista ellos gastan.
Volviendo a este ejemplo, usamos la fórmula para la prueba T para muestra Única,
que es, Z= ( Entonces, en este ejemplo, la media, Esta calculadora de Prueba T de Comparación de Medias de Dos Muestras calcula la prueba T
de comparación de medias de dos muestras.
Esta prueba se usa cuando la variable es numérica (por ejemplo, el costo de los bienes, las
ganancias, el precio de las acciones) y se están comparando dos poblaciones o grupos.
Se deben seleccionar dos muestras aleatorias separadas, una de cada población, para calcular la prueba T resultante.
La fórmula para calcular la estadística de prueba que compara dos medias poblacionales es,
Z= ( Para calcular la estadística, debemos calcular los medios de la muestra ( Luego procedemos encontrando la diferencia entre los medios de muestra ( Luego calculamos √(σx2/n1 + σy2/n2), cual es el error estándar.
Luego dividimos la diferencia de los medios por este error estándar.
Repasemos una práctica. Digamos que tenemos una muestra aleatoria de 40 automóviles de cada compañía
en la que estamos comparando dos compañías. Estos son autos eléctricos y queremos medir qué tan lejos puede
llegar cada auto una vez que está completamente cargado. Supongamos que las millas promedio que puede recorrer Tesla son
200 millas con una desviación estándar de 1,2 y las millas promedio que puede recorrer la hoja de nissan son 190 millas con una desviación estándar de 1,5.
Teniendo en cuenta esta información, Ahora tenemos todos nuestros datos para calcular la prueba T que compara dos medias de población. Conectándolos a nuestra fórmula, nos da
Z= ( La prueba T de una proporción calcula la prueba T cuando
la variable es categorial (por ejemplo, género, trabajadores/desempleados, demócratas/republicanos)
y solo se está estudiando una población.
La prueba busca la proporción de individuos en la población que tienen una determinada característica, por ejemplo, la proporción de mujeres que tienen hijos.
La hipótesis nula es H0:p=p0, donde p0 es un cierto valor reclamado.
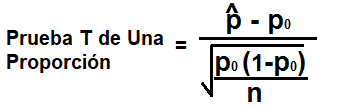
La fórmula para la prueba T de una proporción es, Z= (ṗ - p0)/√p0(1-p0)/n
ṗ representa el número de personas en la misma población que tienen una característica particular
de interés (por ejemplo, el número de mujeres que actualmente están embarazadas en la población). p0 es el valor
declarado para la hipótesis nula. n es el tamaño de la muestra.
Entonces, digamos que hay mujeres que van al OBGYN cada mes y de ellas, un médico afirma que el 80% de ellas están actualmente embarazadas en el momento de su visita. La población son mujeres que van al Ginecólogo y las mujeres que están embarazadas son la proporción de la población. La afirmación es que el 80% (p = 0,8) están embarazadas cuando visitan. Sospecha que la cantidad de mujeres embarazadas es menor que esto (< 0,8).
Supongamos que 75 de las 100 mujeres incluidas en la muestra estaban embarazadas, quien fueron a la oficina de OBGYN.
Tenga en cuenta que ṗ es igual a la proporción de la muestra, lo que significa que en este caso es igual a, ṗ= 75/100= 0,75
Conectando estos valores en la fórmula, Z= (ṗ - p0)/√p0(1-p0)/n= (0,75- 0,8)/√(0,8)(1-0,8)/100= -1,25
La Calculadora de prueba T de Dos Proporciones calcula
la prueba T cuando la variable que se prueba es categoritcal y le interesa
en la proporción de individuos con una cierta característica de 2 categorías diferentes, como el género (masculino/femenino).
Digamos que estamos interesados en estudiar a personas con anemia de
células falciformes; esta es la proporción específica de la
población que queremos estudiar. A diferencia de una sola proporción de una población,
estudiamos ambas categorías de esta población en lugar de solo una. Con una sola proporción de una población,
estudiaríamos la población masculina o femenina que tienen anemia de células falciformes.
Con dos proporciones de población, estudiamos dos poblaciones o grupos (como hombres y mujeres con anemia falciforme).
Para realizar esta prueba, se deben seleccionar dos muestras aleatorias separadas, una
de cada población (en nuestro caso, hombres y mujeres con anemia de células falciformes).
La fórmula para calcular la prueba T para dos proporciones de población es,
Z= ṗ1 - ṗ2/√ṗ(1-ṗ)(1/n1 + 1/n2)
ṗ1 y ṗ2 son las proporciones de la muestra.
Para cada muestra, el tamaño de muestra es n1 y n2
(no es necesario que sean iguales). ṗ es la proporción de muestra agrupada, que es el número total de
individuos de ambas muestras que tienen la característica de interés dividida por el número total de individuos
de ambas muestras (n1 + n2 ).
Entonces, como un ejemplo, digamos que hay un grupo de examinandos.
De los examinados, 8/241 que bebieron mucho café antes de la prueba no aprobaron el examen.
4/220 que no tomó café antes de la prueba no pasó el examen. Calculemos la prueba T de dos proporciones de población.
En base a este ejemplo, los datos son
ṗ1= 8/241= 0,033,
ṗ2= 4/206= 0,019, n1= 241,
n2= 220,
and ṗ= (4+8)/(141+206)= 12/347= 0,03458.
Conectando estos valores en la fórmula,
Z= ṗ1 - ṗ2/√ṗ(1-ṗ)(1/n1 + 1/n2)=
(0,033 - 0,019)/√0,03458(1-0,03458)(1/241 + 1/206)= 0,80750601371697
Para utilizar cualquiera de estas calculadoras, un usuario simplemente ingresa en todos los
diversos campos y la prueba T resultante se mostrará a continuación.
Si desea calcular la prueba T basada en muestras de datos emparejados, consulte nuestra
Calculadora de Prueba T para Muestras Relacionadas
Si desea calcular la prueba T basada en muestras de datos no apareados, consulte nuestra
Calculadora de Prueba T para Muestras Independientes
Recursos Relacionados
Calculadora de Valor de p
Calculadora de Prueba T de Comparación de Medias de Dos Muestras

Calculadora de Prueba T de Una Proporción
Calculadora de Prueba T de Dos Proporciones
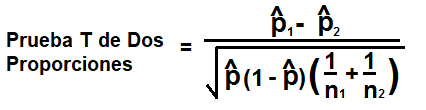
Calculadora de Valor Esperado
Calculadora de Teorema de Chebyshev
Calculadora de Intervalo de Confianza
Calculadora de Prueba de Hipótesis Estadística
Calculadora de Valor T
Calculadora de Puntaje Z a Puntaje Bruto
