Calcolatrice di Test di Verifica di Ipotesi
Questa calcolatrice de verifica d'ipotesi determina se un'ipotesi alternativa è vera o meno. In base al fatto che sia vero o no determina se accettiamo o rifiutiamo l'ipotesi. Accettiamo ipotesi vere e rifiutiamo ipotesi false.
L'ipotesi nulla è l'ipotesi che viene rivendicata e che andremo a verificare.
L'ipotesi alternativa è l'ipotesi che pensiamo che sia davvero.
Ad esempio, supponiamo che un'azienda affermi di ricevere solo 20 reclami dei consumatori in un anno medio. Tuttavia, riteniamo che molto probabilmente riceverai molto di più. In questo caso l'ipotesi nulla è l'ipotesi rivendicata dalla società, che la media dei reclami è 20 (μ = 20). L'ipotesi alternativa è che μ> 20, che è ciò che sospettiamo. Quindi, quando facciamo i nostri test, vediamo quale ipotesi è veramente vera, quella nulla (dichiarata) o l'alternativa (ciò che pensiamo che sia).
Il livello di significatività selezionato determinerà la larghezza di un'area che sarà l'area di rifiuto. Il livello di significatività è rappresentativo dell'area di rifiuto totale di una normale curva standard. Se scegli di calcolare con un livello di significatività dell'1%, scegli una distribuzione normale standard con un'area di rifiuto dell'1% del 100% totale. Se scegli un livello di significatività del 5%, l'area di rifiuto aumenta del 100% al 5%. Se scegli un livello di significatività del 20%, aumenta il range della curva normale standard al 20% del 100%. Maggiore è il livello di significatività, maggiore è l'area di rifiuto. Ciò significa che c'è una maggiore probabilità che un'ipotesi venga rifiutata e meno propensa ad accettarla, poiché l'area di accettazione diminuisce. Pertanto, maggiore è il livello di significatività, minore o minore è l'area di accettazione. Più basso è il livello di significatività, maggiore è l'area di non rifiuto.
Esistono 3 tipi di test di ipotesi che possiamo eseguire.
C'è una coda sinistra, una coda destra e un test di ipotesi a due code.
Coda Sinistra
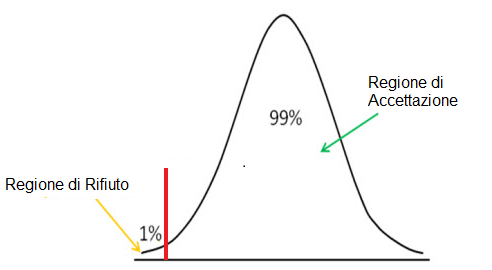
Il test de verifica d'ipotesi sulla coda sinistra è illustrato di seguito::

Usiamo i test di ipotesi della coda di sinistra per vedere se il punteggio z è al di sopra del punto de taglio del livello di significatività, nel qual caso accettiamo l'ipotesi nulla come vera.
Il metodo della coda sinistra, come la coda destra, ha un punto di taglio. Il livello di significatività scelto determina questo punto di taglio. Qualsiasi valore al di sotto di questo punto di taglio nel metodo della coda sinistra rappresenta l'area di rifiuto. Ciò significa che se otteniamo uno punteggio z al di sotto del punto di taglio, il punteggio z sarà nell'area di rifiuto. Ciò significa che l'ipotesi è falsa. Se il punteggio z è al di sopra del punto di taglio, significa che si trova nell'area di accettazione e accettiamo l'ipotesi come vera.
Il metodo della coda sinistra viene utilizzato se si desidera determinare se
una media campionaria è inferiore alla media dell'ipotesi. Ad esempio, supponiamo che la media dell'ipotesi sia di
$40.000, che rappresenta lo stipendio medio degli addetti ai servizi igienico-sanitari,
e vogliamo determinare se questo stipendio è diminuito negli ultimi anni.
Ciò significa che vogliamo vedere se la media del campione è inferiore alla media dell'ipotesi di $40.000.
Questo è un test classico dell'ipotesi della coda sinistra, dove la media del campione,
Coda Destra
Il test di verficia d'ipotesi sulla coda destra è illustrato di seguito:
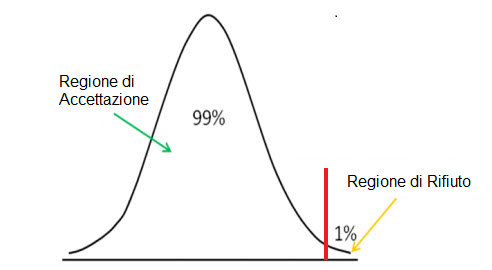
Usiamo i test di ipotesi della coda di destra per vedere se il punteggio z è inferiore al punto di taglio del livello di significatività, nel qual caso accettiamo l'ipotesi nulla come vera.
Il metodo della coda destra, come la coda sinistra, ha un punto di taglio. ' Il livello di significatività scelto determina questo punto di taglio. Qualsiasi valore al di sopra di questo limite nel metodo della coda destra rappresenta l'area di rifiuto. Ciò significa che se otteniamo uno punteggio z al di sopra del punto di taglio, il punteggio z sarà nell'area di rifiuto. Ciò significa che l'affermazione dell'ipotesi nulla è falsa. Se il punteggio z è inferiore al punto di cut-off, significa che si trova nell'area di accettazione e accettiamo l'ipotesi come vera.
Il metodo della coda di destra viene utilizzato se vogliamo determinare se una media campionaria
è maggiore della media dell'ipotesi. Ad esempio, supponiamo che un'azienda affermi di subire 400 infortuni
sul lavoro all'anno. Ciò significa che l'ipotesi nulla è 400. Tuttavia, sospettiamo che tu abbia molti più incidenti
di questo. Pertanto, vogliamo determinare se questo numero di incidenti è maggiore di quanto dichiarato.
Ciò significa che vogliamo vedere se la media del campione è maggiore della media dell'ipotesi di 400.
Questo è un test classico dell'ipotesi della coda destra, dove la media del campione,
Due Code
Di seguito è riportato un test di verifica d'ipotesi a due code:
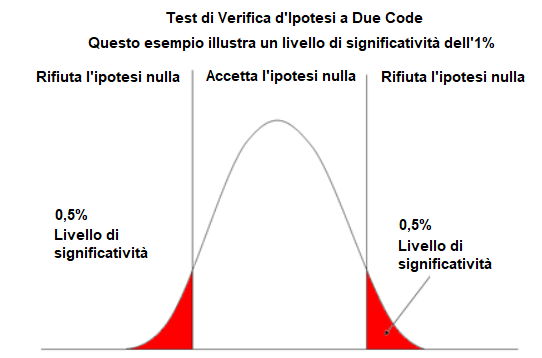
Usiamo il metodo a due code per vedere se la media campionaria effettiva non è uguale a quanto affermato nella media dell'ipotesi.
Pertanto, se la media dell'ipotesi è da intendersi 100. L'ipotesi alternativa può affermare che la media del campione non è 100.
Il metodo a due code ha 2 punti di taglio. Il livello di significatività scelto determina questi punti di taglio . Se scegli un livello di significatività dell'1%, le due estremità della curva normale rappresenteranno lo 0,5% per rappresentare il livello di significatività dell'1%. Se scegli un livello di significatività del 5%, i 2 estremi della curva normale comprenderanno ciascuno il 2,5% per compensare gli estremi.
Se il punteggio z calcolato è compreso tra i 2 estremi, accettiamo l'ipotesi nulla e rifiutiamo
l'ipotesi alternativa. Questo perché il punteggio z sarà nell'area di accettazione.
Se lo il punteggio z è al di fuori di questo intervallo, rifiutiamo l'ipotesi nulla e
accettiamo l'alternativa perché è al di fuori dell'intervallo.
Pertanto, la media del campione è effettivamente diversa dalla media dell'ipotesi nulla, che è la media dichiarata.
Per utilizzare questo calcolatore, un utente seleziona la media dell'ipotesi nulla (la media dichiarata), la media del campione, la deviazione standard, la dimensione del campione e il livello di significatività e fa clic sul pulsante "Calcola". La risposta risultante verrà calcolata automaticamente e visualizzata di seguito, con una spiegazione della risposta.
Il test di ipotesi può essere utilizzato per qualsiasi tipo di scienza per mostrare se rifiutiamo o accettiamo un'ipotesi basata sul calcolo quantitativo. Anche in alcune aree dell'elettronica, potrebbe essere utile.
Risorse Correlate
Calcolatrice di Notazione Scientifica
Calcolatrice di Cifre Significative
Calcolatrice di Arrotondamento delle Cifre Significative
Calcolatrice Fattorizzazione
Calcolatrice dell'Intervallo di Confidenza
Calcolatrice del Valore Atteso
Calcolatrice di Teorema di Bernoulli
Calcolatrice di Teorema di Chebyshev
Calcolatrice di Test T per Dati Appaiati
