Gleichungssystem Rechner
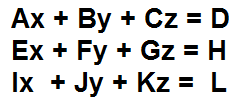
1x1 Gleichungssystem Rechner
Beispiel:
2x=6
Der 1x1 Gleichungssystemrechner berechnet die Lösung für eine lineare Gleichung, die eine Variable enthält.
1x1-Gleichungssystem haben die Form Ax = B, wobei A der Koeffizient der Variablen und B der Wert ist, dem die Gleichung entspricht.
Um diesen Rechner zu verwenden, muss ein Benutzer lediglich den Koeffizienten vor der
Variablen, die in diesem Fall mit X bezeichnet ist, und den Wert eingeben, dem die Gleichung entspricht.
Beispiel
Ein Beispiel für eine 1x1-Lineargleichung ist:
3x=6
Lösung:
x=2
Der in diesem Fall eingegebene Koeffizient ist 3 und der Wert, dem die Gleichung entspricht, ist 6. Wenn wir 6 nehmen und durch 3 teilen, erhalten wir unsere Lösung, die x= 2 ist.
Das 1x1-Gleichungssystem ist die einfachste aller linearen Gleichungen.
2x2 Gleichungssystem Rechner
Beispiel:
1x + 2y=3
4x + 5y=6
Der 2x2 Gleichungssystem Rechner berechnet die Lösung für 2 lineare Gleichungen mit 2 Variablen.
2x2 lineare Gleichungen nehmen die Form an:
Ax + By=C
Dx + Ey= F
dabei sind A, B, D und E die Koeffizienten der Variablen und C und F die Werte, denen die Gleichungen entsprechen.
Um diesen Rechner verwenden zu können, muss ein Benutzer lediglich die Koeffizienten
vor den Variablen eingeben, die in diesem Fall mit X und Y bezeichnet werden, sowie die Werte,
denen die Gleichungen entsprechen.
Beispiel
Ein Beispiel für eine lineare 2x2-Gleichung ist:
x + 2y=3
4x + 5y=6
Lösung:
x=-1, y=2
Die Koeffizienten, die in diesem Fall eingegeben werden,
sind 1, 2, 4 und 5, und die Werte, denen die Gleichungen entsprechen,
sind 3 und 6. Wenn wir die erste Gleichung nehmen und nach x auflösen,
erhalten wir x= 3-2y. Wir nehmen dann diese Gleichung und stecken sie in die zweite
Gleichung und erhalten 4 (3-2y) + 5y = 6. Wenn wir dies lösen, erhalten wir 12-8y + 5y = 6.
Dies entspricht -3y = -6. Somit ist y = 2. Da wir jetzt wissen, dass y = 2 ist,
können wir dies in jede der Gleichungen einfügen, um nach X zu lösen.
Wenn wir die erste Gleichung verwenden, x + 2y = 3, erhalten wir x + 2(2)= 3. Somit ist x = -1.
3x3 Gleichungssystem Rechner
Beispiel:
1x + 2y + 5z=3
4x + 5y + 8z=6
7x + 8y + 3z=5
Der 3x3 Gleichungssystem Rechner berechnet die Lösung für 3 lineare Gleichungen mit 3 Variablen.
3x3 lineare Gleichungen haben folgende Form:
Ax + By + Cz=D
Ex + Fy + Gz=H
Ix + Jy + Kz=L
wobei A, B, C, E, F, G, I, J und K die Koeffizienten der Variablen sind und D, H und L sind die Werte, denen die Gleichungen gleich sind.
Um diesen Rechner verwenden zu können, muss ein Benutzer lediglich die Koeffizienten
vor den Variablen eingeben, die in diesem Fall mit X, Y und Z bezeichnet werden, sowie die Werte,
denen die Gleichungen entsprechen.
Beispiel
Ein Beispiel für eine lineare 3x3-Gleichung ist:
x + 2y + 4z=4
2x + 5y + 12z=8
9x + 10y + 6z=20
Lösung:
x=-28, y=32, z=-8
Die Koeffizienten, die in diesem Fall eingegeben werden, sind 1, 2, 4, 2, 5, 12, 9, 10 und 6 und die Werte, die die Gleichungen sind gleich sind 4, 8 und 20. Wieder können wir durch Substitution nach X, Y und Z lösen. Wenn wir die erste Gleichung nehmen und nach Z auflösen, erhalten wir Z = (4-x-2y)/4. Wir nehmen nun diesen Z-Wert und stecken ihn in die nächste Gleichung. Auf diese Weise erhalten wir 2x + 5y +12 (4-x-2y/4). Wenn wir nach y auflösen, erhalten wir y = 4-x. Wir können dies nun in die endgültige Gleichung einfügen. Wir stecken 4-x für y und (4-x-2 (4-x)) / 4 für z ein. Wir machen eine doppelte Substitution für die letzte, so dass wir nur x Variablen in der letzten Gleichung haben. Wenn wir nach X auflösen, erhalten wir x = -28. Da wir wissen, dass x = -28 und y = 4-x ist, wissen wir, dass y = 32. Wenn Sie nun -28 für x und 32 für y in eine der Gleichungen einfügen, erhalten Sie -8 für z.
Substitution ist eine der besten und einfachsten Methoden zur Lösung von Gleichungssystemen.
Das Gleichungssystem wird in vielen verschiedenen technischen und elektronischen
Anwendungen eingesetzt. Zwei solche Anwendungen sind die Netzstromanalyse und die
Spannungsschleifenanalyse von Kirchhoff.
Bei der Lösung von Maschenströmen (KCL) und Kirchhoffs Spannungsschleife (KVL)
sind Gleichungssysteme die gebräuchlichste und am weitesten verbreitete Methode
zur Lösung dieser Strom- und Spannungswerte.
Ähnliche Resourcen
Signifikante Stellen Rechner
Runden Signifikante Stellen Rechner
Wissenschaftliche Schreibweise Rechner
Faktorisierung Rechner
Erwartungswert Rechner
Konfidenzintervall Rechner
Hypothesentest Rechner
Tschebyscheff-Ungleichung Rechner
Bernoulli Ungleichung Rechner
Korrelationskoeffizient Rechner
Gleichungssystem Rechner
Gewicht auf dem Mond Rechner
Partielle Ableitung Rechner
