Korrelationskoeffizient Rechner
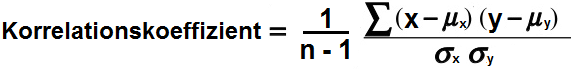
Dieser Korrelationskoeffizienten rechner berechnet die Stichprobenkorrelation zwischen 2 Variablen.
Die Probenkorrelation ist ein Maß für die Stärke und Richtung der linearen Beziehung zwischen zwei quantitativen Variablen.
Die klassische Situation der 2 quantitativen Variablen sind (x, y) Paare.
Die Stichprobenkorrelation misst das Ausmaß der Beziehung zwischen jeder der x- und y-Werte für die gegebenen (x, y) -Paare.
Wenn eine Linie entweder linear linear ist oder eine perfekte lineare positive Steigung hat, dann ist die Stichprobenkorrelation 1. 1 stellt eine perfekte Linearität dar.
Wenn eine Linie vollkommen vertikal ist, geradeaus und linear, dann ist die Stichprobenkorrelation 0.
Wenn eine Linie vollkommen linear ist und eine negative Steigung hat, dann ist die Stichprobenkorrelation -1.
So dienen diese nur als Referenzpunkte für Beispiel-Korrelationsvariablen.
Also lasst uns jetzt in die Formel für die Beispielkorrelation einsteigen. Die Formel zur Berechnung des Korrelationskoeffizienten ist also wie folgt: Korrelationskoeffizient= (1/n-1)∑(x-μx) (y-μy)/σxσy
Um also den Korrelationskoeffizienten zu lösen, müssen wir die Mittelwerte und die Standardabweichung der x-Werte und der y-Werte berechnen.
Wir werden jetzt alle Schritte zur Lösung für den Korrelationskoeffizienten durchlaufen.
Also das erste ist, dass wir den Mittelwert für die x-Werte und die y-Werte berechnen müssen.
Der Mittelwert für die x-Werte kann entweder durch μx oder
Danach müssen wir die Standardabweichungen für die x- und y-Werte berechnen. Die Standardabweichung für die x-Werte wird durch σx dargestellt und die Standardabweichung für die y-Werte wird durch σy dargestellt. Die Standardabweichung für die x-Werte wird durch Subtrahieren des Mittelwerts von jedem der x-Werte, Quadrieren dieses Ergebnisses, Addition aller Quadrate, Teilen dieser Zahl durch die n-1 (wobei n die Anzahl der Elemente ist) und dann die Quadratwurzel dieses Ergebnisses zu nehmen. Das gleiche gilt für y-Werte.
Danach nehmen wir für jedes (x, y) Paar im Datensatz jeden x Wert und subtrahieren
Wir teilen diese Summe dann durch das Produkt der Standardabweichungen, σx und σy.
Schließlich teilen wir das Ergebnis mit n-1, wobei n die Anzahl der gepaarten (x, y) Datenpunkte ist.
Beispiel
Jetzt, wo du die Schritte kennst, um zu tun, lasst uns eigentlich ein Beispiel machen.
So wie ein Beispiel, nehmen wir die Datenpunkte (2,7), (8,12), (11,17)
Die Standardabweichung für die x-Werte σx beträgt 4,58. Die Standardabweichung für die y-Werte σy beträgt 5.
Wir nehmen dann jeden der x-Werte und minus
Das Hinzufügen jedes dieser gibt uns, (25+20)=45
Das Produkt der Standardabweichungen für x und y (σy * σy), gibt uns, (4,58*5)=22,9
45/22,9 = 1,965
Schließlich teilen wir diese Zahl mit n-1 auf. Damit, (1,965/2)= 0,98
Um diesen Rechner zu benutzen, tritt ein Benutzer einfach in die x- und
y-Wertpaare ein. Ein Benutzer kann überall von 3 bis 10 (x, y) Wertpaaren eingeben. Danach
klickt der Benutzer auf 'Berechnen' und der erwartete Wert
wird berechnet und automatisch angezeigt.
Ähnliche Ressourcen
Signifikante Stellen Rechner
Runden Signifikante Stellen Rechner
Wissenschaftliche Schreibweise Rechner
Faktorisierung Rechner
Erwartungswert Rechner
Konfidenzintervall Rechner
Hypothesentest Rechner
Tschebyscheff-Ungleichung Rechner
Bernoulli Ungleichung Rechner
Gleichungssystem Rechner
Gewicht auf dem Mond Rechner
